Differential Equations and Bifurcation Theory

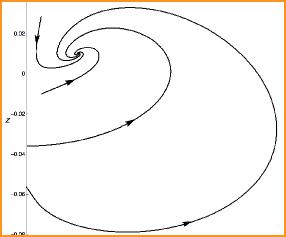
Differential equations are mathematical models that describe many of the phenomena we experience in nature and in our every day lives. Part of my research program involves studying these types of equations, with particular attention to how the solutions of these equations change as external parameters are varied. In mathematical terminology, this is called bifurcation theory.

The goal is to use this knowledge in order to provide helpful insight into the physical phenomenon that is being modeled by the differential equations.

Interactions of waves with inhomogeneities

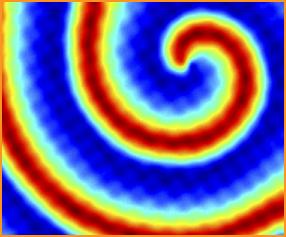
I am particularly interested in differential equations models which describe the propagation of electrical signals in biological tissue, such as the heart muscle or the neurons that compose the brain and nervous system. In this case, solutions describe waves which propagate in the biological medium. Very simple models for these phenomena suppose that the medium of propagation is uniform (or homogeneous and isotropic). However, reality is much more complicated than that.

Imperfections (such as diseased tissue) can lead to pathological conditions, such as re-entrant (spiral) waves in cardiac tissue. This is a common cause of tachycardia and ventricular fibrillations, conditions which can be fatal. Part of my research program involves studying the effects of inhomogeneities and/or anisotropy on the propagation of waves in excitable media such as the heart muscle or the nervous system.

Functional Differential Equations

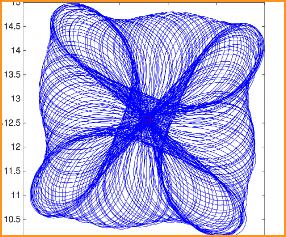
Closely related to the program described above, I also study a special class of differential equations, called delay-differential equations, which are frequently used as models for biological systems in which time-delays are present.

The nervous system is a marvelous example of such a system. In this case, there is a time delay involved between the perception of a signal by the sensory organs, transmission of this signal to the brain, its treatment and processing by the brain, and then on to other parts of the body. These equations are also used to model drug delivery in patients, machine chattering of tools, disease outbreaks, vaccination strategies, etc. My efforts in this area have involved developing analytical tools to study these equations, with the goal of shedding light on the behavior of the biological or physical system being modeled by these equations. Currently, I am investigating structured delay systems. These are models that are frequently used to study population dynamics, and take into account the various stages of development and/or sizes of the population, e.g. juveniles vs adults.