
MAT 3775 - Analyse de la régression
Table des matières
Télécharger et installer R
Exemple 1 : Travailler à la console
Exemple 2 : Affection d'une variable
Exemple 3 : L'éditeur de R.
Exemple 4 : Statistiques descriptives (univariées)
Exemple 5 : Statistiques descriptives (bivariées)
Exemple 6 : Loi de probabilité
Exemple 7 : Importer des données d'un fichier
Exemple 8 : Nuage de points et la surperposition d'une courbe lisse
Exemple 9 : Opérations sur une colonne
Exemple 10 : Ajuster un modèle linéaire avec la fonction lm
Exemple 12 : L'analyse de variance avec un objet lm
Exemple 13 : Un test F partiel pour comparer deux modèles
Exemple 14 : Une variable explicative binaire
Exemple 15 : La signification d'une corrélation
Exemple 21 : Introduction au modèle de régression linéaire multiple (aussi dit modèle linéaire)
Exemple 23 : Comparer des modèles emboités pour tester des hypothèses (Test F partiel)
Exemple 24 : Test de la signifcation de la régression
Exemple 25 : La loi F non-centrée et la puissance
Exemple 31 : La régression polynomiale
Exemple 32 : Une spline linéaire
Exemple 33 : Interaction entre prédicteurs
Exemple 34 : Test de l'inadéquation de l'ajustement (Test for lack-of-fit)
Exemple 35 : Diagnostique
Exemple 36 : Diagnostique pour l'homoscédascité
Exemple 37 : Correction de White pour l'hétéroscédasticité
Exemple 38 : Diagnostique pour la normalité
Exemple 39 : Construire un modèle
Exemple 40 : Aberrance en X et en Y -- Influence
Télécharger et installer R
Exemple 1 : Travailler à la console
Ci-dessous, on a un affiche de la console de R. Nous entrons des commandes à l'invite >.
Nous pouvons utiliser R comme une calculatrice. Nous avons calculé (1/8)*ln(2^3)+5. La réponse est 5,25993.
Il y a une console dans Rstudio. C'est dans la fenêtre en bas à gauche.
Exemple 2 : Affection d'une variable
Exemple 3 : L'éditeur de R
-
Le moyen le plus efficace de travailler en R est d'ouvrir une fenêtre d'édition.
- Sélectionner File -> New Script (en Windows) ou File -> New Document (sur un Mac).
- Nous pouvons écrire un script (une suite de commandes) dans l'éditeur de R.
- Pour soumettre le script, sélectionnez les commandes (avec la souris) que vous souhaitez soumettre.
- Pour soumettre la sélection, appuyez sur CTRL-R (sous Windows) ou appuyez sur CTRL-ENTER (sur un Mac).
- Pour ouvrir une fenêtre d'édition avec Rstudio, sélectionnez File -> New File -> R Script.
- Nous pouvons écrire un script (une séquence de commandes) dans la fenêtre d'édition.
- Pour soumettre le script à la console, sélectionnez les commandes (avec votre souris).
- Pour soumettre la sélection, appuyez sur le bouton Run situé au dessus de la fenêtre d'édition ou appuyez sur CTRL-ENTER (avec Windows) ou appuyez sur CMD-ENTER (avec un Mac).
Exemple 4 : Statistiques Descriptives (univariées)
Soit x un vecteur numérique. Pour notre exemple, considérons l'attribution suivante :
x=c(16,15,14,16,13,12,14,13,10)
- La fonction summary dans R produit un sommaire numérique. Son utilisation est
summary(x)
Voici une sortie de R qui démontre l'affection des valeurs au vecteur numérique et l'utilisation de la fonction summary.
> x=c(16,15,14,16,13,12,14,13,10)
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
10.00 13.00 14.00 13.67 15.00 16.00
- Il est possible d'obtenir chacune des statistiques descriptives individuellement.
- Voici une liste de commandes pour certaines statistiques descriptives communes :
sum(x) # pour la somme
mean(x) # pour la moyenne
var(x) # pour la variance
sd(x) # pour l'écart type
min(x) # pour le minimum
max(x) # pour le maximum
median(x) # pour la médiane
quantile(x) # pour certain quantiles
length(x) # pour le nombre de composantes dans le vecteur
- Comme exemple, on calcul la moyenne, l'écart type et certains centiles (minimum, premier quartile, médiane, troisième quartile et
maximum).
> mean(x)
[1] 13.66667
> sd(x)
[1] 1.936492
> quantile(x)
0% 25% 50% 75% 100%
10 13 14 15 16
- Plusieurs méthodes non-paramétriques sont basées sur les rangs. On ordonne les n valeurs du plus petit au plus grand et on utilise
les rangs de 1 à n. Pour des égalilés, on utilise le rang moyen. La fonction rank, nous donne les rangs. Voici un exemple.
> x
[1] 16 15 14 16 13 12 14 13 10
> rank(x)
[1] 8.5 7.0 5.5 8.5 3.5 2.0 5.5 3.5 1.0
Parfois on veut réellement ordonner les valeurs. On peut le faire avec la fonction sort. On obtient les statistiques
d'ordre. Voici un exemple. > x
[1] 16 15 14 16 13 12 14 13 10
> sort(x)
[1] 10 12 13 13 14 14 15 16 16
Remarque: La fonction sort utilise un arrangement en ordre croissant par défaut. On peut utiliser utiliser l'argument
decreasing = TRUE pour obtenir un arrangement en ordre décroissant. Voici un exemple.
> sort(x,decreasing=TRUE)
[1] 16 16 15 14 14 13 13 12 10
Exemple 5 : Statistiques Descriptives (bivariées)
Considérons les deux variables numériques suivantes : y=nombres de rhumes en 6 ans et x=la dose journalière de vitamine C (en mg). Voici
l'attribution des valeurs dans R.
y<-c(16,15,14,16,13,12,14,13,10)
x<-c(0,0,0,25,25,25,50,50,50)
- On peut utiliser la commande
plot(x,y) pour produire un nuage de points pour décrire l'association entre ces deux variable
numériques. En utilisant la commande suivante
> plot(x,y,xlab="Dose de vitamine C (en mg)",ylab="Nombre de rhumes")
nous avons produit le nuage de point ci bas.
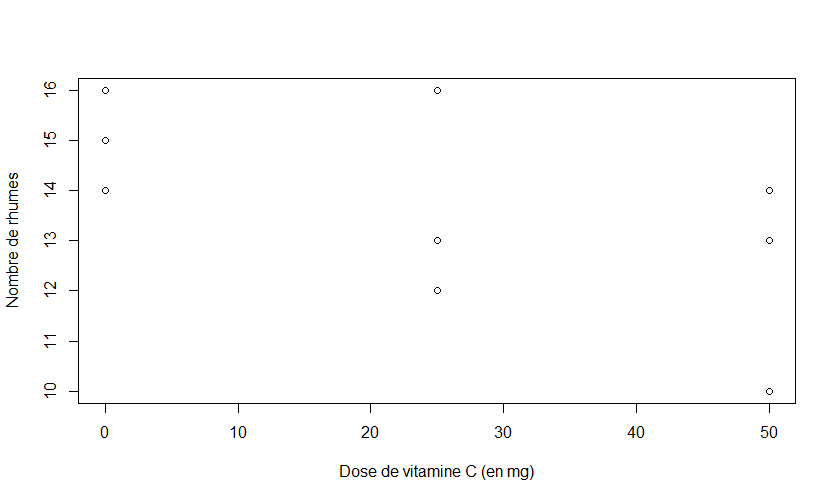
- Pour calculer la covariance et la corrélation entre
x et y, on peut utiliser les commandes cov et cor.
Voici la sortie de R.
> cov(x,y)
[1] -25
> cor(x,y)
[1] -0.5962848
- Par défaut, R calcul la corrélation de Pearson. Mais on peut ajouter un argument dans la fonction pour obtenir la corrélation de
Spearman. Voici un exemple.
> cor(x,y,method="spearman")
[1] -0.5871366
Remarque: La corrélation de Spearman est la corrélation de Pearson entre les rangs de x et les rangs de y.
Exemple 6 : Loi de probabilités
| Loi de probabilités | Nom en R | arguments |
| béta | beta | shape1, shape2, ncp |
| binomiale | binom | size, prob |
| Cauchy | cauchy | location, scale |
| khi-deux | chisq | df, ncp |
| exponentielle | exp | rate |
| F | f | df1, df2, ncp |
| gamma | gamma | shape, scale |
| géométrique | geom | prob |
| hypergéometric | hyper | m, n, k |
| log-normale | lnorm | meanlog, sdlog |
| logistique | logis | location, scale |
| binomiale négative | nbinom | size, prob |
| normale | norm | mean, sd |
| Poisson | pois | lambda |
| rang signé | signrank | n |
| t de Student | t | df, ncp |
| uniforme | unif | min, max |
| Weibull | weibull | shape, scale |
| Wilcoxon | wilcox | m, n |
Le tableau ci-haut contient certaines lois de probabilités en R. On utilise le nom de la loi avec un préfixe. Voici la liste des préfixes:
- d pour la densité de probabilité;
- p pour la fonction de répartition;
- q pour la fonction de quantile (l'inverse de la fonction de répartition);
- r pour générer des valeurs au hasard de cette loi.
Voici quelques exemples de son utilisation.
Supposons qu'on veut calculer P(Z>1.65), P(U>12.6), P(T>1.71) et P(F>1.85), où Z suit une loi N(0,1), U suit une loi khi-deux avec 6 degrés de liberté, T suit une loi
t(24) et F suit une loi F(20,15). Voici les commandes.
> 1-pnorm(1.65)
[1] 0.04947147
> 1-pchisq(12.6,6)
[1] 0.04984649
> 1-pt(1.71,24)
[1] 0.05008269
> 1-pf(1.85,20,15)
[1] 0.1140452
Alors, P(Z>1.65)=0.049471, P(U>12.6)=0.0498469, P(T>1.71)=0.05008269, P(F>1.85)=0.1140452.
Le quantile d'ordre p (pour la variable aléatoire X) est une valeur q tel que F(q)=P(X<=q)=p. [Si X est discrète, alors c'est la plus petite quantité q tel que
P(X<=q)>=p.] Par exemple, considérons t(0,975;43), qui est le quantile d'ordre 0,975 de la loi t avec 43 degrés de liberté. Alors, si
T est une variable aléatoire t(43), alors P[T<=t(0,975;43)]=0,975. La commande pour obtenir t(0,975;43) est ci-bas.
> qt(0.975,43)
[1] 2.016692
Alors t(0,975;43)=2.016692.
Supposons qu'on veut générer 10 valeurs d'une loi normale de moyenne 46 et d'écart type 7. Voici la commande.
> rnorm(10,46,7)
[1] 46.93336 55.43874 39.04338 56.84523 52.93618 39.41287 31.94741 43.18834
[9] 45.07614 51.84981
Exemple 7 : Importer des données d'un fichier
Nous allons sauvegarder nos données dans un fichier de format CSV (c'est-à-dire un fichier avec des colonnes délimitées par des virgules).
Commentaires:
Exemple 8 : Nuage de points avec une courbe lisse
Exemple: Dans le fichier cerveaux.csv, nous avons n = 25 espèces de mamifères (les rangés). Nous avons deux variables
pour décrire chacune des espèces : masse (en grammes), et gestation (en jours). Nous importons le fichier et nous affichons quelques rangés avec la fonction head.
> cerveau<-read.csv("cerveaux.csv")
> head(cerveau)
masse..grammes. gestation..en.jours.
1 10 50
2 10 55
3 12 56
4 12 75
5 12 85
6 45 86
En supposant que x et y sont des vecteurs numériques, on peut utiliser la fonction plot(x,y) pour construire un nuage de point de y contre x.
Avec la commande suivante, nous allons construire un nuage de point de la masse du cerveau à la naissance contre la durée de la période de gestation.
with(cerveau, plot(gestation..en.jours.,masse..grammes.,xlab="Gestation (en jours)",ylab="Masse du cerveau (en grammes)"))
Voici le nuage de points.
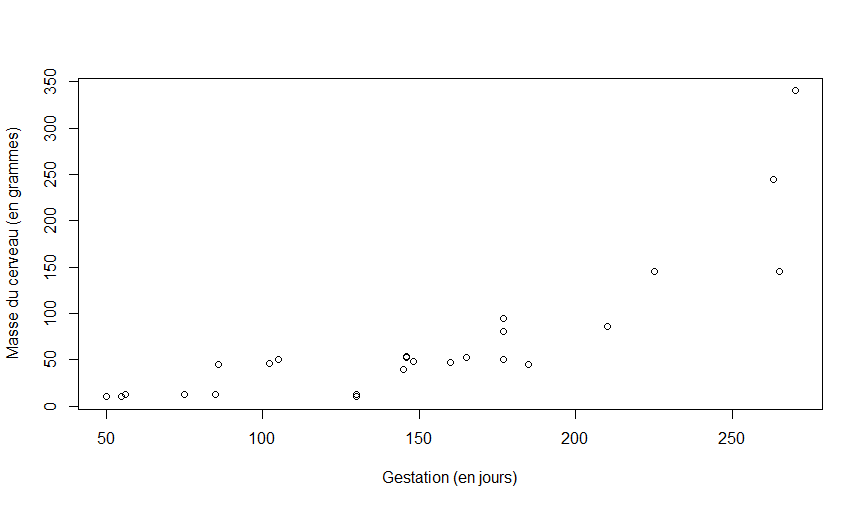
Afin de mieux visualier le lien entre les deux variables nous pouvons ajouter une courbe lisse au diagramme.
## ajuster une courbe lisse (loess=lowess=locally weighted scatterplot smoothing)
mod.loess<-loess(masse..grammes.~gestation..en.jours.,data=cerveau)
## obtenir l'étendue pour x
range(cerveau$gestation..en.jours.)
## construire un nouveau jeu de données
new.data<-data.frame(gestation..en.jours.=seq(50,270,by=10))
## add Lowess Smooth to the plot
with(new.data,lines(x=gestation..en.jours.,y=predict(mod.loess,new.data),lty=2))
Commentaires:
- La commande
lines(x,y) ajoute au nuage de points un nuage de points de y contre x tel qu'on a des segments de droite entre le points successifs.
- L'argument
lty décrit le type de ligne qui sera utilisé.
- Avec la fonction
data.frame, on a construit un nouveau jeu de données qui contient une colonne qui a le même nom que notre variable x.
- La fonction
predict(object, newdata) évalue un modèle estimé object aux valeurs dans le jeu de données newdata.
Voici le nuage de points avec la superposition d'une courbe lisse.
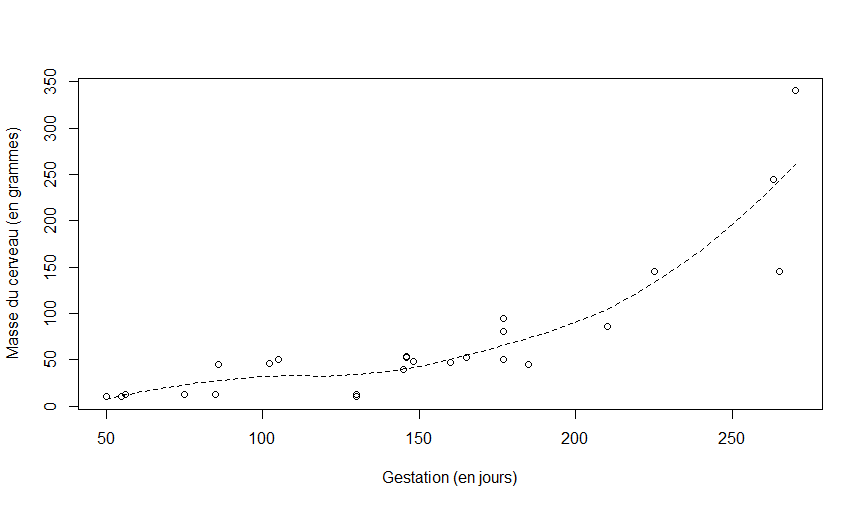
Corrélation de Spearman:
-
La corrélation entre la masse du cerveau et la durée de la période de gestation est r=0.81. Ceci est la corrélation de Pearson. Elle est une description de l'intensité d'une association linéaire entre deux variables numériques. Ici le lien n'est pas linéaire, alors c'est difficile à interpréter la corrélation. C'est mieux d'utiliser la corrélation de Spearmen quand le lien est monotone et non-linéaire.
> with(cerveau,cor(gestation..en.jours.,masse..grammes.))
[1] 0.8113314
- Par défaut, la fonction
method="pearson". On peut plutôt utiliser l'argument method="spearman" pour obtenir la corrélation de Spearman. (C'est la corrélation de Pearson entre les rangs de x et les rangs de y.)
- La corrélation entre la masse du cerveau et la durée de la période de gestation est rS=0.86.
> with(cerveau,cor(gestation..en.jours.,masse..grammes.,method="spearman"))
[1] 0.8628308
N.B.: Pour visualiser la linéarité ou non-linéarité d'une association entre deux variables numériques, nous pouvons aussi superimposer une droite estimée sur le nuage de points. On peut utiliser la fonction lm pour obtenir la droite des moindres carrés et utiliser la fonction abline pour ajouter cette droite au nuage de points. Pour ajouter la droite au nuage de points et aussi une légende, on utilise les commandes suivantes:
# estimer la droite
mod<-lm(masse..grammes.~gestation..en.jours.,data=cerveau)
# ajouter la droite au diagramme
abline(mod)
legend("topleft",legend=c("droite estimée","courbe lisse"),
lty=c(1,2),inset=0.05)
Voici le diagramme résultant.
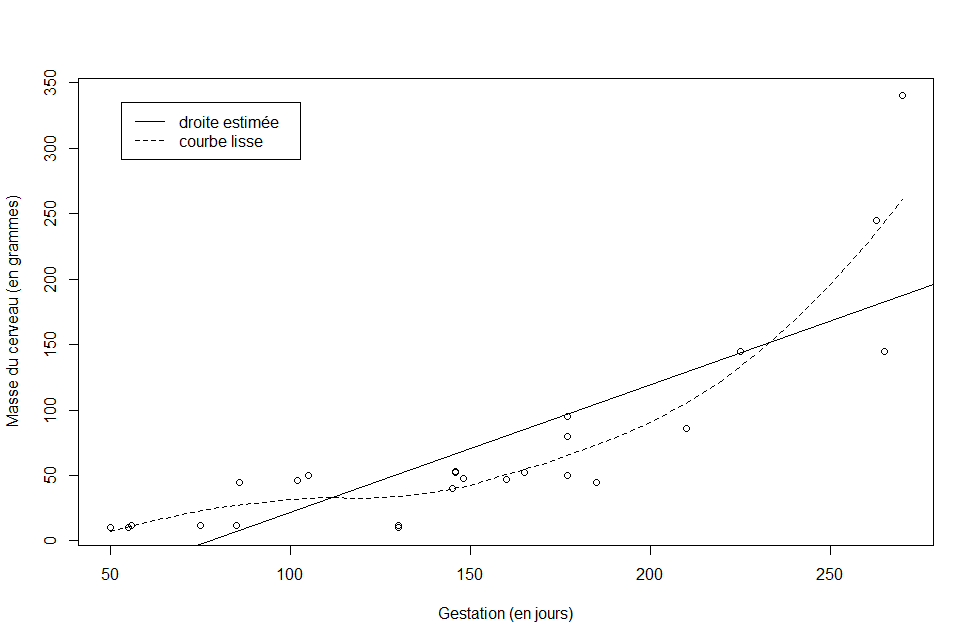
Exemple 9 : Opérations sur une colonne et transformations d'une variable
Soient x et y des variables numérique ayant le même nombre de rangés. Soit a un scalaire (c-à-d un nombre).
Remarque: La plupart des opérations sur les colonnes sont définies par rangée (c'est-à-dire par composante).
a+x # additionne a à chaque composante
a*x # multiplier a à chaque composante
x/a # diviser chaque composante par a
x+y # addition par composante
x*y # multiplication par composante
log(x) # appliquer ln à chaque composante
sqrt(x) # appliquer la racine carrée à chaque composante
x^a # appliquer la puissance à chaque composante
abs(x) # appliquer la valeur absolue à chaque composante
Voici quelques fonctions pratiques :
sum(x) # la somme des composantes de x
length(x) # le nombre de composantes
Exemple : Considérons l'échantillon aléatoire suivant : 10, 12, 11, 12, 15, 20, 16. Calculons la variance de l'échantillon en utilisant les opérations sur les colonnes. Ensuite vérifions notre calcul avec la fonction var.
> x=c(10, 12, 11, 12, 15, 20, 16)
> sum((x-mean(x))^2)/(length(x)-1)
[1] 12.2381
> var(x)
[1] 12.2381
Rappel: La définition de la variance de l'échantillon est
s2=∑ni=1(xi−x¯)2n−1.
Là considérons la variable y=c(11, 12, 11, 13, 14, 18, 17). Calculons la covariance entre x et y avec les opérations sur les colonnes. Ensuite vérifions nos calculs avec la fonction cov.
> sum((x-mean(x))*(y-mean(y)))/(length(x)-1)
[1] 9.404762
> cov(x,y)
[1] 9.404762
Rappel: La définition de la covariance de l'échantillon est x et y est
σ^X,Y=∑ni=1(xi−x¯)(yi−y¯)n−1.
Exemple [Carburant] : Considérons les données dans le fichier evaporation.csv. Ce sont des mesures de la vélocité dans l'air (en cm/s) et du coefficient d'évaporation de carburant (en mm2/s)
brûlant dans un moteur d'impulsion. Utilisons la notation suivante : x=la vélocité et y=l'évaporation du carburant.
On importe les données avec R et on affiche quelques rangés.
> carburant<-read.csv("evaporation.csv")
> head(carburant)
Velocite Evaporation
1 20 0.18
2 60 0.37
3 100 0.35
4 140 0.78
5 180 0.56
6 220 0.75
Nous calculons les sommes suivantes avec R:
∑i=1nxi=2220; ∑i=1nyi=9,1; ∑i=1ny2i=9,6722; ∑i=1nx2i=580400; ∑i=1nxiyi=2340,4.
> x<-carburant$Velocite
> y<-carburant$Evaporation
> sum(x)
[1] 2220
> sum(y)
[1] 9.1
> sum(x^2)
[1] 580400
> sum(y^2)
[1] 9.6722
> sum(x*y)
[1] 2340.4
Exemple 10 : Ajuster un modèle linéaire avec la fonction lm
Exemple [Carburant] : Considérons les données dans le fichier evaporation.csv. Ce sont des mesures de la vélocité dans l'air (en cm/s) et du coefficient d'évaporation de carburant (en mm2/s)
brûlant dans un moteur d'impulsion. Utilisons la notation suivante : x=la vélocité et y=l'évaporation du carburant.
On importe les données avec R et on affiche quelques rangés.
> carburant<-read.csv("evaporation.csv")
> head(carburant)
Velocite Evaporation
1 20 0.18
2 60 0.37
3 100 0.35
4 140 0.78
5 180 0.56
6 220 0.75
On peut utiliser la fonction lm pour ajuster le modèle linéaire pour décrire l'évaporation du carbutant un fonction de la vélocité dans l'air.
> mod<-lm(Evaporation ~ Velocite, data=carburant)
> mod
Call:
lm(formula = Evaporation ~ Velocite, data = carburant)
Coefficients:
(Intercept) Velocite
0.059033 0.003807
Alors, le modèle linéaire estimé est Evaporationˆ=0.059033+0.003807velocité.
Commentaires:
- Nous avons construit un objet
lm que nous avons nommé mod. Cet objet contient a plusieurs composantes qu'on peut afficher en utilisant la fonction names.
> names(mod)
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign" "qr"
[8] "df.residual" "xlevels" "call" "terms" "model"
La première composantes est le vecteur des esimations des betas. Alors, b0=0.059032967 et b1=0.003806593.
> mod$coefficients
(Intercept) Velocite
0.059032967 0.003806593
La deuxième composante est le vecteur des résidus et la 8ième composante est le nombre de degrés de liberté des résidus. On peut les utilisés pour calculer l'estimation de la variance de l'erreur, c'est-à-dire MSE=∑ni=1e2i/(n−2)=0.02512. L'écart type de cette variance est dite l'écart type résiduelle se=MSE−−−−√=0.1584 mm2/s. Ceci est une description d'un écart type de la droite.
> MSE<-sum(mod$residuals^2)/mod$df.residual
> MSE; sqrt(MSE)
[1] 0.02511653
[1] 0.158482
- Il y a plusieurs fonctions qu'on puisse utiliser avec un object
lm. Pour afficher ces fonctions, on peut utiliser la fonction methods.
> methods(class=lm)
[1] add1 alias anova case.names coerce
[6] confint cooks.distance deviance dfbeta dfbetas
[11] drop1 dummy.coef effects extractAIC family
[16] formula hatvalues influence initialize kappa
[21] labels logLik model.frame model.matrix nobs
[26] plot predict print proj qr
[31] residuals rstandard rstudent show simulate
[36] slotsFromS3 summary variable.names vcov
see '?methods' for accessing help and source code
Voici une description de l'ajustment avec le maximum du log la fonction de vraisemblance
ℓ=−n2ln(2πSSE/n)−n/2=5,758624.
Il y a 3 degrés de liberté, puisque nous avons 3 paramètres à estimer β0,β1 et σ2.
> logLik(mod)
'log Lik.' 5.758624 (df=3)
V\'erifions que R ait bien utilis\'e la formule ci-haut pour calculer le maximum du log la fonction de vraisemblance.
> ## p=2=le nombre de paramètres dans la fonction de la moyenne
> p<-length(mod$coefficients)
> ## n = (n-p) + p = degrés de liberté de l'erreur + p
> n<-mod$df.residual+p
> ## SSE = somme des carrés résiduelle
> SSE<-sum(mod$residuals^2)
> # calculons le max du log de la vraisemblance
> -n/2*log(2*pi*SSE/n)-n/2
[1] 5.758624
- On peut obtenir des intervalles de confiance pour les estimations des param\`etres.
> confint(mod)
2.5 % 97.5 %
(Intercept) -0.16731971 0.285385640
Velocite 0.00282118 0.004792006
Commentaires:
-
Le niveau de confiance est 95% par défaut. Mais, on peut modifier l'argument
level pour changer le niveau de confiance.
> confint(mod,level=0.98)
1 % 99 %
(Intercept) -0.223281643 0.341347577
Velocite 0.002577553 0.005035633
- On peut aussi spécifier les paramètres qui nous intéressent. Supposons qu'on veut seulement un IC pour la pente.
> confint(mod,parm=c("Velocite"))
2.5 % 97.5 %
Velocite 0.00282118 0.004792006
- On peut obtenir un sommaire de l'ajustement avec la fonction
summary.
> summary(mod)
Call:
lm(formula = Evaporation ~ Velocite, data = carburant)
Residuals:
Min 1Q Median 3Q Max
-0.18422 -0.14648 0.04483 0.13786 0.18804
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0590330 0.1000605 0.590 0.57
Velocite 0.0038066 0.0004356 8.739 1.09e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1585 on 9 degrees of freedom
Multiple R-squared: 0.8946, Adjusted R-squared: 0.8829
F-statistic: 76.36 on 1 and 9 DF, p-value: 1.086e-05
Commentaire: - Ce n'est pas nécessaire d'afficher toute le sommaire. Le sommaire lui-même est un objet avec des composantes.
> names(summary(mod))
[1] "call" "terms" "residuals" "coefficients" "aliased" "sigma"
[7] "df" "r.squared" "adj.r.squared" "fstatistic" "cov.unscaled"
Voici l'estimations des paramètres et le test de la signification pour chacun.
> summary(mod)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.059032967 0.1000605427 0.5899725 5.697228e-01
Velocite 0.003806593 0.0004356076 8.7385826 1.085924e-05
On peut afficher le coefficient de détermination R2=89,5%.
> summary(mod)$r.squared
[1] 0.8945677
On peut afficher l'écart type résiduelle se=MSE−−−−√=0,158482.
> summary(mod)$sigma
[1] 0.158482
Exemple 12 : L'analyse de variance avec un objet lm
Exemple: Considérons les données sont dans le fichier suivant: VC.csv. Sauvegarder le fichier dans votre répertoire de travail (current working directory).
Rappel: C'est une étude avec des volontaires en bonne santé. Un stimulus est appliqué aux doigts du
sujet et on mesure la vitesse de conduction de la moelle épinière (VC). On veut décrire l'association entre la taille
de l'indivu (en cm) et la vitesse de conduction de la moelle épinière pour les individus en bonne santé.
On importe les données avec R et on affiche quelques rangés.
> VC <- read.csv("VC.csv")
> head(VC)
Taille.en.cm VC
1 149 14.4
2 149 13.4
3 155 13.5
4 155 13.5
5 156 13.0
6 156 13.6
Utilisons un modèle linéaire simple pour décrire la vitesse de conduction de la moelle épinière en fonction de la taille de l'individu (en cm). La fonction de la moyenne est
E[Y|X=x]=β0+β1x.
Nous voulons tester pour la signification de la taille de l'individu en confrontant
H0: β1=0 contre Ha: β1≠0.
(Puisque nous avons un modèle simple, ceci est aussi dit un test pour la signification de la régression.) Nous pouvons tester ces hypothèses avec la statistique t∗=b1/s{b1}. Mais, une autre approche est d'utiliser une analyse de variance (ANOVA).
Pour obtenir le tableau d'ANOVA, on peut mettre l'objet lm dans la fonction anova.
> mod<-lm(VC ~ Taille.en.cm, data=VC)
> anova(mod)
Analysis of Variance Table
Response: VC
Df Sum Sq Mean Sq F value Pr(>F)
Taille.en.cm 1 287.56 287.563 391.3 < 2.2e-16 ***
Residuals 153 112.44 0.735
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Commentaires:
- La statistique du test est F=391,3. Ceci veut dire que l'estimation de la variance de l'erreur basée sur la somme des carrés de la régression est 391,\!3 fois aussi grande que l'estimation de la variance de l'erreur basée
sur la somme des carrés résiduelle. Il est fort probable que MSR n'estime pas σ2, mais plut\^ot quelque chose de plus grand.
On peut d\'emontrer que
E{MSR}=E{SSR}=σ2(1+β21sxx).
Ceci veut dire que nous avons des preuves que β1≠0.
- Pour avoir une mesure de la signification des preuves contre H0:β1=0, on calcul nos chances d'avoir observer une statistique F aussi grande que 391,3 en supposant que H0 est vraie. Sous H0, F∗∼F(1,n2), alors
la valeur P est
P(F(1,153)>391,3)<0,0001.
- Le test basé sur T et l'analyse de variance sont équivalents, puisqu'on peut démontrer que
t∗=(b1s{b1})2=SSR/1SSE/(n−2)=F et t21−α/2;n−2=F(1−alpha;1,n−2).
Exemple 13 : Un test F partiel pour comparer deux modèles
Exemple: Considérons les données sont dans le fichier suivant: VC.csv. Sauvegarder le fichier dans votre répertoire de travail (current working directory).
Rappel: C'est une étude avec des volontaires en bonne santé. Un stimulus est appliqué aux doigts du
sujet et on mesure la vitesse de conduction de la moelle épinière (VC). On veut décrire l'association entre la taille
de l'indivu (en cm) et la vitesse de conduction de la moelle épinière pour les individus en bonne santé.
On importe les données avec R et on affiche quelques rangés.
> VC <- read.csv("VC.csv")
> head(VC)
Taille.en.cm VC
1 149 14.4
2 149 13.4
3 155 13.5
4 155 13.5
5 156 13.0
6 156 13.6
Utilisons un modèle linéaire simple pour décrire la vitesse de conduction de la moelle épinière en fonction de la taille de l'individu (en cm). La fonction de la moyenne est
E[Y|X=x]=β0+β1x.
Nous voulons tester pour la signification de la taille de l'individu en confrontant
H0: β1=0 contre Ha: β1≠0.
(Puisque nous avons un modèle simple, ceci est aussi dit un test pour la signification de la régression.) Nous pouvons tester ces hypothèses avec la statistique t∗=b1/s{b1}.
Nous allons vous présenter une autre approche au test dit le test F partiel, qui est une comparaison de modèles. Si H0:β1=0 est vraie, alors nous imposons une contrainte \`a l'espace des param\`etres et ceci réduit le modèle.
La fonction de la moyenne du modèle réduit est
E[Y|X=x]=β0.
Alors, voici une autre façon d'écrire les hypothèses\:
H0: E[Y|X=x]=β0 contre Ha: E[Y|X=x]=β0+β1x.
Pour évaluer les preuves contre H0 en faveur de Ha, nous allons comparer l'ajustement des deux modèles tel que décrit par la somme des carrés résiduelles. Avec R, on ajuste les deux modèles et pour les comparer on met les deux objets dans la fonction anova.
> mod<-lm(VC ~ Taille.en.cm, data=VC)
> ## modele réduit
> mod0<-lm(VC ~ 1, data=VC)
> mod<-lm(VC ~ Taille.en.cm, data=VC)
> ## modele réduit
> mod0<-lm(VC ~ 1, data=VC)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: VC ~ 1
Model 2: VC ~ Taille.en.cm
Res.Df RSS Df Sum of Sq F Pr(>F)
1 154 400.00
2 153 112.44 1 287.56 391.3 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Nous comparons la somme des carrés du modèle complet SSE=112,44 à la somme des carrés du modèle réduit SSE(R)=400,00, en calculant la somme des carrés supplémentaires
ExtraSS=SSE(R)−SSE=287.56.
Plus que cette somme de carrés supplémentaire est grande, plus que nous considérerons le modèle réduit comme étant moins bien ajusté en comparaison au modèle complet. Si ces preuves sont fortes, alors nous avons des preuves contre H0 en faveur de Ha que la pente est non-nulle.
Exemple 14 : Une variable explicative binaire
Exemple [Azote] : Une étude fut menée sur le développement de l'ectomycorhizue, une relation symbiotique entre
les racines des arbres et un champignon, dans lequel les minéraux sont transférés du champignon aux arbres et du
sucre des arbres au champignon, 20 semis de chênes rouges du nord exposés au champignon pisolithus tinctorus ont
été cultivés dans une serre. Toutes les semis ont été plantées dans le même type de terre et ont reçu la même quantité
de soleil et d'eau. La moitié des semis (choisis au hasard) ont reçu un traitement de 368 ppm d'azote sous la forme
NaNO3. Les autres semis n'ont pas reçu d'azote. La masse de la tige, en grammes, est mesurée après 140 jours. Les
données sont dans le fichier Azote.csv.
Nous importons les données et nous affichons quelques rangés. On remarque que la variable Azote est une variable catégorique.
> azote<-read.csv("Azote.csv")
> head(azote)
Masse Azote
1 0.59 non
2 0.47 non
3 0.25 non
4 0.36 non
5 0.42 non
6 0.19 non
Affichons les catégories de la variable Azote. R considère la première catégorie comme la catégorie de référence. Alors, ne pas avoir reçu de l'azote est considéré comme le groupe de référence. On peut changer l'ordre des catégories afin que le groupe de traitement d'azote soit le groupe de référence avec la fonction factor.
> levels(azote$Azote)
[1] "non" "oui"
> azote$Azote<-factor(azote$Azote, levels=c("oui","non"))
> levels(azote$Azote)
[1] "oui" "non"
Commentaire: Si nous avons un groupe de contrôle, c'est ce groupe qui est souvent utilisé comme le groupe de référence. Alors, nous allons changer l'ordre afin que le groupe sans azote soit le groupe le premier groupe.
> azote$Azote<-factor(azote$Azote, levels=c("non","oui"))
Voici des statistiques descriptives pour la masse de la tige (y) pour chacun des groupes.
> aggregate(Masse~Azote,data=azote,FUN=mean)
Azote Masse
1 non 0.392
2 oui 0.628
> aggregate(Masse~Azote,data=azote,FUN=var)
Azote Masse
1 non 0.01355111
2 oui 0.01819556
> aggregate(Masse~Azote,data=azote,FUN=length)
Azote Masse
1 non 10
2 oui 10
En alternatif, on peut utiliser la fonction tapply.
> moyenne<-with(azote,tapply(Masse,Azote,mean))
> variance<-with(azote,tapply(Masse,Azote,var))
> n<-with(azote,tapply(Masse,Azote,length))
> data.frame(moyenne,variance,n)
moyenne variance n
non 0.392 0.01355111 10
oui 0.628 0.01819556 10
Remarque: Avec la commande tapply(y,x,FUN), on évalue la fonction FUN sur la variable y selon les niveaux de la variable x.
En supposant que le groupe de contrôle soit le groupe 1 et que le groupe de traitement soit le groupe 2, on a
y¯1=0,392; y¯2=0,628; s21=0,013551; s22=0,018196; n1=n2=10.
Si on suppose que les variances des deux populations sont égales, alors on peut estimer cette variance avec la variance pondérée
s2p=(n1−1)s21+(n2−1)s22n1+n2−2=0,014286.
Avec R :
> ## variance poindérée
> sum(variance*(n-1)/sum(n))
[1] 0.014286
Pour comparer les deux groupes visuellement, on peut utiliser des diagrammes à boîte comparatifs avec une superposition de points.
boxplot(Masse~Azote,data=azote,ylab="Masse",
names=c("Sans azote","Avec azote"))
stripchart(Masse~Azote,data=azote,method="jitter",
vertical = TRUE,add=TRUE)
Voici le diagramme correspondant.
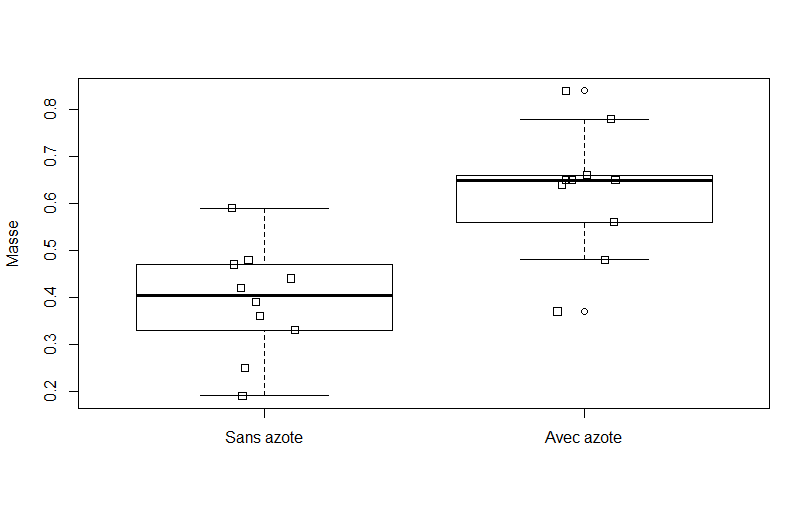
On peut utiliser un test T de Student pour comparer les deux moyennes. La valeur observée de la statistique du test est
t∗=y¯1−y¯2sp1/n1+1/n2−−−−−−−−−−√=−4,1885.
La valeur p est 2P(T(18)>|−4,1885|)=0,0005521.
Avec R :
> t.test(Masse~Azote,data=azote,var.equal=TRUE)
Two Sample t-test
data: Masse by Azote
t = -4.1885, df = 18, p-value = 0.0005521
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.3543747 -0.1176253
sample estimates:
mean in group non mean in group oui
0.392 0.628
On peut utiliser une approche de régression pour faire ce test. (Ceci va nous aider à généraliser le test à la comparaison de plus que 2 groupes plus tard.)
Pour identifier les groupes, nous allons utiliser une variable muette (dummy variable en anglais)~:
xi={1,0,group de traitementsinon.
Consid\'erons le modèle de régression linéaire simple: Y1,Y2,…,Yn sont normales, ind\'ependantes tel que
E[Yi]=β0+β1xi={β0=μ1,β0+β1=μ2,xi=0xi=1
et $V[Y_i]=\sigma^2. Alors, nous avons deux populations normales indépendantes avec des variances égales.
Quand notre variable explicative est une variable catégorique (ceci est dit factor dans la terminologie de R), alors R va coder des variables muettes correspondantes. Pour afficher ces variables muettes, on utilise la fonction contrasts.
> contrasts(azote$Azote)
oui
non 0
oui 1
On interprète la variable de la façon suivante. Ceci est utilisé pour identifier la catégorie oui. Elle est égale à 0, si l'unité est non. Elle est égale à 1, si l'unité est oui.
Ajustons le modèle linéaire pour décrire la masse selon le groupe de traitement.
> mod<-lm(Masse~Azote,data=azote)
> mod$coefficients
(Intercept) Azoteoui
0.392 0.236
> summary(mod)$sigma^2
[1] 0.01587333
Alors, notre estimation de la masse moyenne est
μ^Y|X=x=b0+b1x={b0=0.392,b0+b1=0.392+0.236=0.628,x=0x=1
L'estimation de la variance σ2 est MSE=0.01587333. Remarquons que ceci nous donne y¯1, y¯2, et s2p, respectivement.
Remarquons que μ1=μ2 si et seulement si β1=0. Alors tester pour la signification de la variable explicative qui identifie le traitement est interpréter comme un test pour l'égalité des moyennes. La valeur observée de la statistique du test est
t∗=b1/s{b1}=4,1885 et la valeur p du test est 2P(T(18)>|4,1885|)=0,0005521.
> summary(mod)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.392 0.03984135 9.839024 1.145796e-08
Azoteoui 0.236 0.05634418 4.188543 5.520945e-04
Exemple 15 : Inférence concernant une corrélation
Exemple [VC] : Considérons les données sont dans le fichier suivant: VC.csv.
Sauvegarder le fichier dans votre répertoire de travail (current working directory).
Rappel: C'est une étude avec des volontaires en bonne santé. Un stimulus est appliqué aux doigts du
sujet et on mesure la vitesse de conduction de la moelle épinière (VC). On veut décrire l'association entre la taille
de l'indivu (en cm) et la vitesse de conduction de la moelle épinière pour les individus en bonne santé.
On importe les données avec R et on affiche quelques rangés.
> VC <- read.csv("VC.csv")
> head(VC)
Taille.en.cm VC
1 149 14.4
2 149 13.4
3 155 13.5
4 155 13.5
5 156 13.0
6 156 13.6
Supposons que nous voulons testez H0:ρ=0 (o\`u ρ est la corrélation (de Pearson) entre la vitesse de conduction et la taille de l'individu) contre Ha:ρ≠0. On peut utiliser la fonction cor.test.
> with(VC,cor.test(Taille.en.cm,VC))
Pearson's product-moment correlation
data: Taille.en.cm and VC
t = 19.781, df = 153, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7967316 0.8869721
sample estimates:
cor
0.8478829
Alors, la valeur observée de la statistique du test est
t∗=rn−21−r2−−−−−−√=19,781.
La valeur p est 2P(T(153)>|19,781|)<0,00001. Les preuves que la corrélation est non-nulle sont significatives.
Commentaires:
- Pour obtenir l'intervalle de confiance pour la corrélation, la fonction
cor.test utilise la transformation z de Fisher. Cette transformation est
12ln(1+r1−r)=arctanh(r).
Fisher a démontré que la distribution d'échantillonage de cette transformation suit approximativement
N(12ln(1+ρ1−ρ),1n−3).
Alors, un IC \`a 95\% pour arctanh(ρ) est
12ln(1+x1−x)±z0,975n−3−−−−−√=[a,b],
où z0,975=1,96. Ensuite en appliquant la fonction inverse qui est
tanh(x)=e2x−1e2x+1,
on obtient un IC pour ρ. Alors, un IC \`a 95\% pour ρ est
[e2a−1e2a+1,e2b−1e2b+1]=[0,797;0,887].
Avec R:
> r<-with(VC,cor(Taille.en.cm,VC))
> z<-qnorm(0.975)
> a<-(1/2)*log((1+r)/(1-r))-z/sqrt(n-3)
> n<-nrow(VC)
> n<-nrow(VC)
> r<-with(VC,cor(Taille.en.cm,VC))
> z<-qnorm(0.975)
> a<-(1/2)*log((1+r)/(1-r))-z/sqrt(n-3)
> b<-(1/2)*log((1+r)/(1-r))+z/sqrt(n-3)
> (exp(2*a)-1)/(exp(2*a)+1)
[1] 0.7967316
> (exp(2*b)-1)/(exp(2*b)+1)
[1] 0.8869721
Exemple 21 : Introduction au modèle de régression linéaire multiple (aussi dit modèle linéaire)
Exemple [Examen SAT en 1999]: Considérons les données de une étude des résultats aux examens SAT aux Etats-Unis en 1999.
Les données sont dans le fichier : sat.csv. On importe les données et on affiche quelques rangés du jeu de données.
> SAT<-read.csv("sat.csv")
> head(SAT)
State Expenditure.per.student student.teacher.ratio Avg.teacher.salary Percent.taking verbalSAT99 mathSAT99 totalSAT99
1 "Alabama" 4.405 17.2 31.144 8 491 538 1029
2 "Alaska" 8.963 17.6 47.951 47 445 489 934
3 "Arizona" 4.778 19.3 32.175 27 448 496 944
4 "Arkansas" 4.459 17.1 28.934 6 482 523 1005
5 "California" 4.992 24.0 41.078 45 417 485 902
6 "Colorado" 5.443 18.4 34.571 29 462 518 980
> dim(SAT)
[1] 50 8
Commentaires: Il y a 50 unités statistiques (les rangés). Les unités sont les 50 états aux Etats-Unis. Nous avons 8 variables pour décrire ces unités. Les trois premières variables sont 3 variables définie au niveau de l'état qui pourrait
être lié aux résultats aux examens du SAT.
Nous voulons étudier le lien entre le revenu moyen des enseignents et les résultats aux SAT (test standardisé
utilisé pour les admissions au collège aux Etats-Unis) en 1999. On observe que l'association entre le salaire moyen et
les résultats aux SAT est significative (p = 0,0031). Cette association est approximativement linéaire, négative avec
une corrélation de r=−R2−−−√=−0,44.
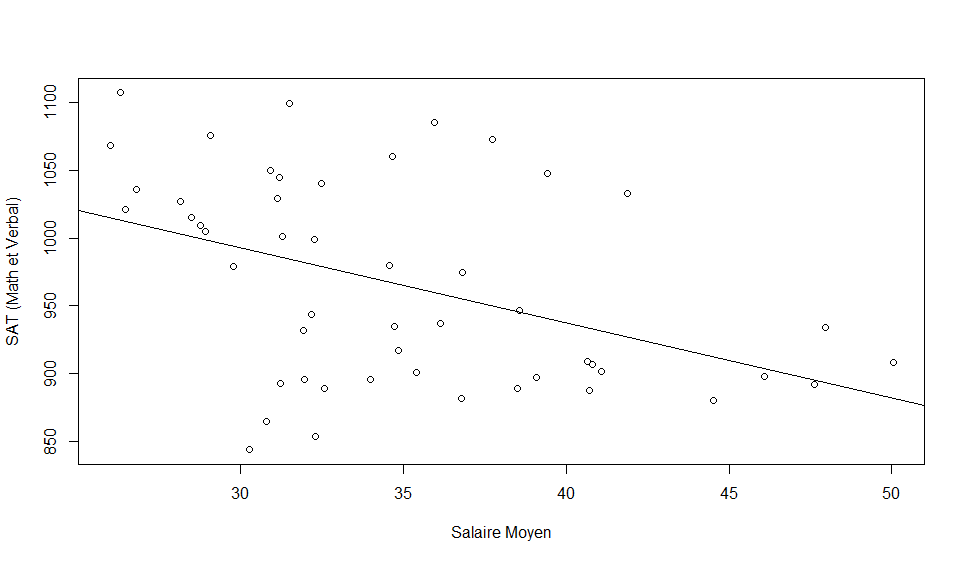
Avec R :
> with(SAT,plot(Avg.teacher.salary,totalSAT99,xlab="Salaire Moyen",ylab="SAT (Math et Verbal)"))
> mod<-lm(totalSAT99~Avg.teacher.salary,data=SAT)
> abline(mod)
> summary(mod)
Call:
lm(formula = totalSAT99 ~ Avg.teacher.salary, data = SAT)
Residuals:
Min 1Q Median 3Q Max
-147.125 -45.354 4.073 42.193 125.279
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1158.859 57.659 20.098 < 2e-16 ***
Avg.teacher.salary -5.540 1.632 -3.394 0.00139 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 67.89 on 48 degrees of freedom
Multiple R-squared: 0.1935, Adjusted R-squared: 0.1767
F-statistic: 11.52 on 1 and 48 DF, p-value: 0.001391
Question : Est-ce que nous avons identifié un lien causal? Est-ce que le salaire élevé des enseignants de certains
états est la cause des résultats médiocres aux tests? Est-ce que certains états devraient réduire le salaire des enseignants
pour améliorer la performance des étudiants aux tests?
Réponse : Non, quand nous observons une association significative entre deux variables, ceci ne veut pas
nécessairement impliquer qu'une est la cause de l'autre. Il peut exister une autre variable qui est liée aux deux
variables et qui explique l'assocation qu'on ait observée. Si une telle variable existe, elle est dite une variable
confusionnelle (confounding variable en anglais).
Variable confusionnelle possible : Essayons de penser à une explication du phénomène ci-haut qui va contre
le bon sense. Il est possible que le taux de participation au test soit lié aux résultats et aux salaires.
Stratification des unités avec une variable muette : La médiane du taux de participation est 28%, alors
nous allons utiliser ce niveau pour définir une variable muette :
MuetteHaut={1;0;taux de participation ≥28%taux de participation <28%
Nous avons diviser les états en 2 groupes : haut taux de participation et faible taux de participation.
Avec R :
> summary(SAT$Percent.taking)
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.00 9.00 28.00 35.24 63.00 81.00
> ## definir une variable muette
> SAT$MuetteHaut<-as.numeric(SAT$Percent.taking>=28)
Commentaire:
- Si nous avions utilisé la commande
SAT$MuetteHaut<-(SAT$Percent.taking>=28), alors nous aurions une variable Booléenne (vrai ou faux) nommé MuetteHaut dans le jeu de données SAT.
- R interprète un vrai comme 1 et un faux comme 0, alors si on force un vecteur Booléen à être numérique, ceci veut dire que TRUE devient 1 et FALSE devient 0.
Voici un nuage de points avec la stratification. Qu'observez-vous?
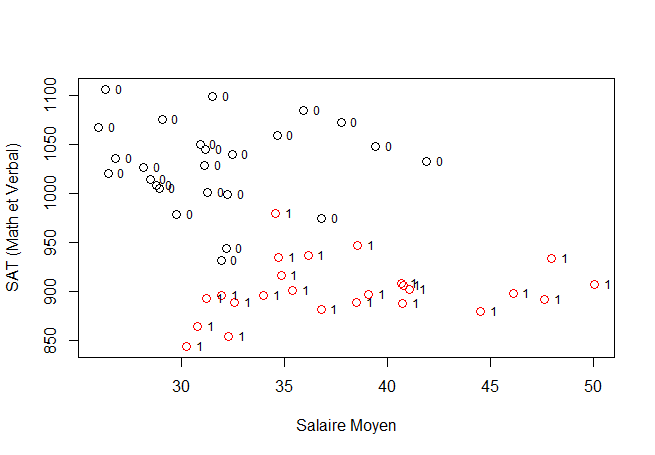
with(SAT,plot(Avg.teacher.salary,totalSAT99,
xlab="Salaire Moyen",ylab="SAT (Math et Verbal)",
col=factor(MuetteHaut), cex=1.25))
with(SAT,text(Avg.teacher.salary,totalSAT99,MuetteHaut,cex=0.75, pos=4))
Un modèle linéaire pour estimer les deux droites: Considérons un modèle linéaire avec 3 variables
indépendantes :
x1=MuetteHaut; x2=Salaire moyen; x3=MuetteHaut * Salaire moyen.
La fonction de la moyenne pour ce mod\`ele est
E{Y}==β0+β1x1+β2x2+β3x3{β0+β1+(β2+β3)(salaire moyen),β0+β2(salaire moyen),MuetteHaut =1MuetteHaut =0
L'estimation par les moindres carrés nous donne:
| Strate |
Ordonnée à l'origine |
Pente |
| MuetteHaut = 1 |
b0+b1=861,05 |
b2+b3=1,0657 |
| MuetteHaut = 0 |
b0=1035,71 |
b2=0,1733 |
Avec R:
> ## fonction I() nous permet d'appliquer des operations
> ## sur des colonnes du dataframe
> mod<-lm(totalSAT99~MuetteHaut+Avg.teacher.salary+I(MuetteHaut*Avg.teacher.salary),data=SAT)
> mod$coefficients
(Intercept) MuetteHaut Avg.teacher.salary
1035.7189251 -174.6680327 -0.1733339
I(MuetteHaut * Avg.teacher.salary)
1.2390482
> OrdHaut=mod$coefficients[1]+mod$coefficients[2]
> PenteHaut=mod$coefficients[3]+mod$coefficients[4]
> OrdBas=mod$coefficients[1]
> PenteBas=mod$coefficients[3]
> ## parametres (estimes) des deux droites
> c(OrdHaut,PenteHaut,OrdBas,PenteBas)
(Intercept) Avg.teacher.salary (Intercept) Avg.teacher.salary
861.0508923 1.0657143 1035.7189251 -0.1733339
Revoici le nuage de points avec la superposition des deux droites.
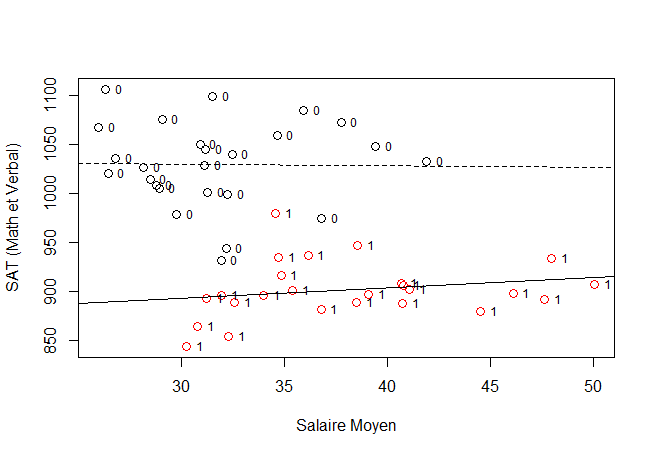
with(SAT,plot(Avg.teacher.salary,totalSAT99,
xlab="Salaire Moyen",ylab="SAT (Math et Verbal)",
col=factor(MuetteHaut), cex=1.25))
with(SAT,text(Avg.teacher.salary,totalSAT99,MuetteHaut,cex=0.75, pos=4))
abline(OrdHaut,PenteHaut)
abline(OrdBas,PenteBas,lty=2)
Taux de participation comme variable quantitative : Dans la pratique, si la variable confusionnelle est une
variable quantitative, alors on devrait l'inclure dans le modèle comme une des variables indépendantes. C'est-à-dire,
on ne devrait pas transformer une variable quantitative en variable catégorique. La plupart du temps ceci cause une dimimution de précision et de puissance.
Nous utilisons un modèle linéaire ou le résultat total aux tests SAT est la variable dépendante et les variables indépendantes
sont le salaire moyen et le taux de participation. La valeur explicative du modèle est décrite avec R2=80,56% et
R2a=79,73%. L'écart type résiduel est se=33,69. L'association entre le taux de participation et les résultats aux tests SAT
est significative et négative. Tandis que l'association entre le salaire moyen des enseignants et le résultat au SAT est
significative et positive.
> mod<-lm(totalSAT99~Avg.teacher.salary+Percent.taking,data=SAT)
> summary(mod)
Call:
lm(formula = totalSAT99 ~ Avg.teacher.salary + Percent.taking,
data = SAT)
Residuals:
Min 1Q Median 3Q Max
-78.313 -26.731 3.168 18.951 75.590
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 987.9005 31.8775 30.991 <2e-16 ***
Avg.teacher.salary 2.1804 1.0291 2.119 0.0394 *
Percent.taking -2.7787 0.2285 -12.163 4e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 33.69 on 47 degrees of freedom
Multiple R-squared: 0.8056, Adjusted R-squared: 0.7973
F-statistic: 97.36 on 2 and 47 DF, p-value: < 2.2e-16
Le modèle linéaire estimée est
Total SATˆ=987,9005+2,1804(Salaire Moyen)−2,7787(Taux de participation (en %)).
Exemple 23 : Comparer des modèles emboités pour tester des hypothèses (Test F partiel)
Considérons un modèle linéaire avec la matrice du plan X de taille n×p. Supposons que nous voulons tester H0 qui nous donne un modèle réduit qui est emboité dans notre modèle. Supposons que X0 de taille n×q est la matrice du plan du
modèle réduit, où les colonnes de X0 appartiennent à l'espace colonne de X. On peut tester H0 avec la statistique F suivante:
F∗=ExtraSS/(p−q)SSE/(n−p), où ExtraSS=SSE(R)−SSE.
Plus que ExtraSS est grande, plus que nous avons des preuves contre H0. Sous H0, la statistique suit une loi F(p−q,n−p). Alors, la valeur-p est P(F(p−q,n−p)>F∗), où F∗ est la valeur observée de la statistique.
Exemple [Rétablissement]: Considérons les données d'une étude observationnelle bio-médicale. Les participants de cette étude
dans une étude a subi une opération du genou. La variable dépendante est le temps de rééducation, et la variable explicative est une variable catégorique décrivant la forme du patient avant une intervention chirurgicale (1 = inférieur à la moyenne; 2 = moyen; 3 = supérieur à la moyenne). Les 24 participants sont des hommes de 18 ans à 30 ans. Nous avons aussi l'âge du participant dans le jeu de données.
Les données sont dans le fichier : genou.csv. On importe les données et on affiche quelques rangés du jeu de données. On change type du vecteur \verb|genou| en vecteur catégorique et on affiche ces niveaux.
> genou<-read.csv("genou.csv")
> head(genou)
Temps Groupe Age
1 29 1 18.3
2 42 1 30.0
3 38 1 26.5
4 40 1 28.1
5 43 1 29.7
6 40 1 27.8
> genou$Groupe<-factor(genou$Groupe)
> levels(genou$Groupe)
[1] "1" "2" "3"
Remarques:
Nous allons utliser un modèle linéaire pour décrire le temps de rétablissement selon la forme. La fonction de la moyenne du modèle linéaire est
\[
E\{Y\}=\beta_0+\beta_1\,\,I\{\mbox{Groupe}=2\} +\beta_2\,I\{\mbox{Groupe}=3\}.
\]
Ici on utilise la notation \(I\) pour une fonction indicatrice, où \(I(A)=1\), si \(A\) est réalisé, sinon \(I(A)=0\). Alors, on a
\[
\begin{eqnarray*}
E\{Y\} &=&\beta_0+\beta_1\,\,I\{\mbox{Groupe}=2\} +\beta_2\,I\{\mbox{Groupe}=3\} \\
&=& \left\{
\begin{array}{ll}
\beta_0=\mu_1, & \mbox{Groupe}=1\\
\beta_0+\beta_1=\mu_2 & \mbox{Groupe}=2\\
\beta_0+\beta_2=\mu_3 & \mbox{Groupe}=3\\
\end{array}
\right.
\end{eqnarray*}
\]
Remarques:
- Alors, l'ordonnée à l'origine \(\beta_0=\mu_1\) est la moyenne du group de référence.
- Alors, le coefficient de la variable muette pour le groupe 2 est \(\beta_1=\mu_2-\mu_1\). Ceci est dit l'effet du groupe 2. C'est la différence entre la moyenne du groupe 2 et le groupe de référence.
- Alors, le coefficient de la variable muette pour le groupe 3 est \(\beta_2=\mu_3-\mu_1\). Ceci est dit l'effet du groupe 3. C'est la différence entre la moyenne du groupe 3 et le groupe de référence.
- Si les effets des groupes 2 et 3 sont nuls, alors ceci veut dire que les moyennes sont égaux, et il y a une moyenne en commune pour les trois groupes. Alors, le test de la signification de la régression que
\[
H_0:\beta_1=\beta_2=0 ~~ \mbox{ contre } ~~ H_a:\beta_1\neq 0 ~~~ \mbox{ ou } ~~~ \beta_2\neq 0
\]
est équivalents aux hypothèses
\[
H_0:\mu_1=\mu_2=\mu_3 ~~ \mbox{ contre } ~~ H_a:~ \mbox{les moyennes ne sont pas égaux}.
\]
Ceci fut la première application d'une ANOVA par R.A. Fisher pour tester l'égalité des moyennes de populations normales et indépendantes.
- Un modèle linéaire qui a seulement des prédicteurs catégoriques est dit un modèle d'ANOVA. Ici nous avons un modèle d'ANOVA à un facteur.
Nous ajustons le modèle d'ANOVA pour décrire le temps de rétablissement selon la forme du patient. Le modèle est significatif \((F(2,21)=16.96; p<0.0001)\).
mod<-lm(Temps~Groupe,data=genou)
> summary(mod)
Call:
lm(formula = Temps ~ Groupe, data = genou)
Residuals:
Min 1Q Median 3Q Max
-9.0 -3.0 -0.5 3.0 8.0
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 38.000 1.574 24.149 < 2e-16 ***
Groupe2 -6.000 2.111 -2.842 0.00976 **
Groupe3 -14.000 2.404 -5.824 8.81e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.451 on 21 degrees of freedom
Multiple R-squared: 0.6176, Adjusted R-squared: 0.5812
F-statistic: 16.96 on 2 and 21 DF, p-value: 4.129e-05
Commentaires:
- On estime que les temps moyens de rétablissement sont
\[
\hat{\mu}_1=38 \mbox{ mois}; ~~ \hat{\mu}_2=38-6=32 \mbox{ mois}; ~~ \hat{\mu}_3=38-14=24 \mbox{ mois}.
\]
L'écart type résiduel est \(s_e=4.451\) mois.
Description: On estime qu'un patient avec un forme inférieure à la moyenne aura en moyenne un temps de rétablissement de 38 mois. Mais, si le patient a une forme moyenne, son temps de rétablissement sera réduite de 6 mois en moyenne. Cette réduction sera 14 mois en moyenne pour les patients ayant un forme supérieure à la moyenne. L'écart type résiduel est de 4,451 mois.
- Avec R, si un modèle linéaire a seulement un prédicteur, alors on peut obtenir le tableau d'ANOVA pour le test de la signifcation de la régression avec la fonction
anova. Ceci est le test de l'égalité des moyennes. On conclue qu'il y a des différences entre les temps moyen de rétablissement selon la forme du patient \((F(2,21)=16.96; p<0.0001)\).
> anova(mod)
Analysis of Variance Table
Response: Temps
Df Sum Sq Mean Sq F value Pr(>F)
Groupe 2 672 336.00 16.962 4.129e-05 ***
Residuals 21 416 19.81
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- On peut aussi obtenir le test de la signification de la régression en utilisant un test linéaire générale. On compare le modèle complet avec le modèle réduit est le modèle \(E\{Y\}=\beta_0\).
> # modèle réduit
> mod0<-lm(Temps~1,data=genou)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: Temps ~ 1
Model 2: Temps ~ Groupe
Res.Df RSS Df Sum of Sq F Pr(>F)
1 23 1088
2 21 416 2 672 16.962 4.129e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- Ici nous avons analysé des données d'une étude observationelle. Il est possible que la différence entre les groupes que nous avons observé peut être expliqué par une variable confusionelle. C'est une pratique commune des études bio-médicales d'ajuster pour l'âge du patient et le sexe du patient. Dans la plupart des cas, l'effet du sexe est très important. Il est aussi une pratique commune de séparer les sexes dans les applications médicales. C'est-à-dire, une étude va souvent seulement avoir des hommes ou seulement des femmes. Les chercheurs de cette étude veulent ajuster pour l'âge. Il est possible que l'âge des patients n'est pas équitablement distribué dans les groupes de la forme. ll est possible qu'on ait plus de patients âgés dans le groupe de forme inférieure à la moyenne, et que c'est ceci qui est la raison qu'on observe des différences entre les groupes. Pour ajuster pour l'âge, on ajoute l'âge comme un prédicteur quantitatif au modèle.
> mod<-lm(Temps~Groupe+Age,data=genou)
> summary(mod)
Call:
lm(formula = Temps ~ Groupe + Age, data = genou)
Residuals:
Min 1Q Median 3Q Max
-1.03891 -0.36892 0.05891 0.33098 0.89991
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.43169 0.86106 8.631 3.54e-08 ***
Groupe2 -1.84738 0.28694 -6.438 2.80e-06 ***
Groupe3 -8.72289 0.33296 -26.198 < 2e-16 ***
Age 1.16729 0.03201 36.461 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5552 on 20 degrees of freedom
Multiple R-squared: 0.9943, Adjusted R-squared: 0.9935
F-statistic: 1170 on 3 and 20 DF, p-value: < 2.2e-16
Remarques:
- Un modèle linéaire avec des prédicteurs quantitatifs et catégoriques est dit un modèle linéaire général. Ici nous avons un modèle linéaire général d'ordre 1 qui décrit le temps de rétablissement selon la forme pré-chirurgie du patient et son âge.
- Le modèle est significatif \(F(3,20)=1170; p<0,\!0001\); \(R^2=0,\!9943\) et l'erreur type résiduelle est 0,5552 mois.
- Le modèle estimée est
\[
\begin{eqnarray*}
\hat{\mbox{temps}} &=& 7,\!43169-1,\!84738\,\,I\{\mbox{Groupe}=2\}-8,\!72289\,I\{\mbox{Groupe}=3\}+1,\!16729\,\mbox{âge}. \\
\end{eqnarray*}
\]
- L'estimation de l'ordonnée à l'origine est $b_0=7,\!43169$. Ceci est le temps de rétablissement pour un patient dans le groupe 1, mais avec un âge de 0. Ceci n'est pas signifiant. Pour donner un sens à l'ordonnée à l'origine, on peut centrer l'âge autour de sa moyenne. L'âge moyen des participants est 23,757 ans. On pourrait centrer autour d'un âge de 24 pour simplifier la description.
> mean(genou$Age)
[1] 23.575
- On ajoute au jeu de données une variable qui sera l'âge centré à 24.
> genou$Age.c<-genou$Age-24
- On ajuste le modèle de nouveau, mais plutôt avec la variable âge centrée.
> mod<-lm(Temps~Groupe+Age.c,data=genou)
> summary(mod)
Call:
lm(formula = Temps ~ Groupe + Age.c, data = genou)
Residuals:
Min 1Q Median 3Q Max
-1.03891 -0.36892 0.05891 0.33098 0.89991
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.44656 0.20842 170.070 < 2e-16 ***
Groupe2 -1.84738 0.28694 -6.438 2.8e-06 ***
Groupe3 -8.72289 0.33296 -26.198 < 2e-16 ***
Age.c 1.16729 0.03201 36.461 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5552 on 20 degrees of freedom
Multiple R-squared: 0.9943, Adjusted R-squared: 0.9935
F-statistic: 1170 on 3 and 20 DF, p-value: < 2.2e-16
Le modèle estimé est
\[
\begin{eqnarray*}
\hat{\mbox{temps}} &=& 35,\!44656-1,\!84738\,\,I\{\mbox{Groupe}=2\}-8,\!72289\,I\{\mbox{Groupe}=3\}+1,\!16729\,(\mbox{âge}-24). \\
&=&\left\{
\begin{array}{ll}
35,\!44656+1,\!16729\,(\mbox{âge}-24), & \mbox{Groupe}=1\\
33,\!59918+1,\!16729\,(\mbox{âge}-24) & \mbox{Groupe}=2\\
26,\,72367+1,\!16729\,(\mbox{âge}-24) & \mbox{Groupe}=3\\
\end{array}
\right.
\end{eqnarray*}
\]
Pour un patient âgé de 24 ans de forme inférieure à la moyenne, on estime que le temps moyen de rétablissement est 35,4 mois. Si ce patient de 24 ans a une forme moyenne, ceci réduit le temps moyen de rétablissement 1,8 mois, et cette réduction est de 8,7 mois pour un patient de 24 ans avec une forme supérieure à la moyenne. Pour chaque année qu'on ajoute à l'âge du patient, on estime que le temps moyen de rétablissement va augmenter de 1,2 mois. L'écart type résiduelle est 0,552 mois.
Exemple 24 : Test de la signification de la régression
Considérons un modèle linéaire avec la fonction de la moyenne suivante
E{Y}=β0+β1x1+…+βp−1xp−1.
Une façon de décrire la valeur explicative du modèle est de vérifier que le modèle est significatif, dans le sense qu'il y a au moins une variable explicative significative.
Le test de la signification de la régression est de confronter
H0 : βj=0, pour j=1,2,…,p−1 contre Ha : βj≠0, pour au moins un j .
La statistique du test est
F∗=MSRMSE=SSR/(p−1)SSE/(n−p),
qui suit une loi F(p−1,n−p) si H0 est vraie. Des grandes valeurs de F∗ sont considéré comme des preuves contre H0.
Exemple [Dwayne Studios]: Nous allons considérer les données dans le fichier Dwayne.csv. Dwayne studios est une compagnie qui a des studios dans n=21 villes de taille moyenne. Leur spécialité est la photographie des enfants. Les variables sont des descriptions des studios dans chacune de ces villes. Elles sont les ventes y, le nombre d'enfants d'\^ages 16 ou moins dans la communaut\'e x1, et
le revenu disponible par habitant x2 (en milliers de dollars).
Le mod\`ele de r\'egression estim\'ee est
y^=−68,8571+0,00145x1+9,3655x2.
> dwayne<-read.csv("Dwayne.csv")
> head(dwayne)
sales num.children disposible.income
1 174.4 68500 16.7
2 164.4 45200 16.8
3 244.2 91300 18.2
4 154.6 47800 16.3
5 181.6 46900 17.3
6 207.5 66100 18.2
> mod<-lm(sales~num.children+disposible.income,data=dwayne)
> coefficients(mod)
(Intercept) num.children disposible.income
-68.85707315 0.00145456 9.36550038
Est-ce qu'on peut utiliser x1 et x2 pour pr\'evoir les ventes dans une autre communit\'e? En d'autres-mots, est-ce que la régression est significative?
On veut tester H0:β1=β2=0 contre Ha: au moins un des coefficients β1,β2 n'est pas zéro.
La statistique du test est
F∗=SSR/(p−1)SSE/(n−p)=99,1
et la valeur-p est P(F(2,18)>99,1)=1,921×10−10. La régression est significative.
> summary(mod)
Call:
lm(formula = sales ~ num.children + disposible.income, data = dwayne)
Residuals:
Min 1Q Median 3Q Max
-18.4239 -6.2161 0.7449 9.4356 20.2151
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.886e+01 6.002e+01 -1.147 0.2663
num.children 1.455e-03 2.118e-04 6.868 2e-06 ***
disposible.income 9.366e+00 4.064e+00 2.305 0.0333 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 11.01 on 18 degrees of freedom
Multiple R-squared: 0.9167, Adjusted R-squared: 0.9075
F-statistic: 99.1 on 2 and 18 DF, p-value: 1.921e-10
Tester pour la signication de la régression avec le test linéaire général: On veut tester H0:β1=β2=0. Ceci est équivalent à confronter
H0:E{Y}=β0 contre Ha:E{Y}=β0+β1x1+β2x2.
Nous ajustons les deux modèles et on les compare avec la fonction anova. La statistique du test est
F∗=Extra/(p−q)SSE/(n−p)=99,103,
et la valeur-p est P(F(2,18)>99,103)=1,92×10−10.
> mod<-lm(sales~num.children+disposible.income,data=dwayne)
> mod0<-lm(sales~1,data=dwayne)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: sales ~ 1
Model 2: sales ~ num.children + disposible.income
Res.Df RSS Df Sum of Sq F Pr(>F)
1 20 26196.2
2 18 2180.9 2 24015 99.103 1.921e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Commentaires: Les deux approches pour le test de la signification de la régression sont équivalentes.
Exemple 25 : La loi F non-centrée
Considérons un test linéaire général avec p=7, q=2 et n=20. La statistique du test F∗ suit une loi F(p−q=5,n−p=13,λ),
o\`u
λ=E{Y}′(H−H0)E{Y}σ2=nf2,
et H est la matrice chapeau du mod\`ele complet et H0 est la matrice chapeau du mod\`ele r\'eduit, et f2 est le f2 de Cohen.
Voici un graphe de la densité de probabilité de la loi F(p−q=5,n−p=13,λ), pour λ=0, λ=1,\lambda=2,et\lambda=3.NousavonsaussisuperimposéunedroiteverticaleàlavaleurcritiqueF(0,\!95;5,13).Rappel:OnrejetteH_0siF^*>F(0,\!95;5,13).Plusque\lambda=n\,f^2estgrand,plusquechancederejetterH_0$ augmente.
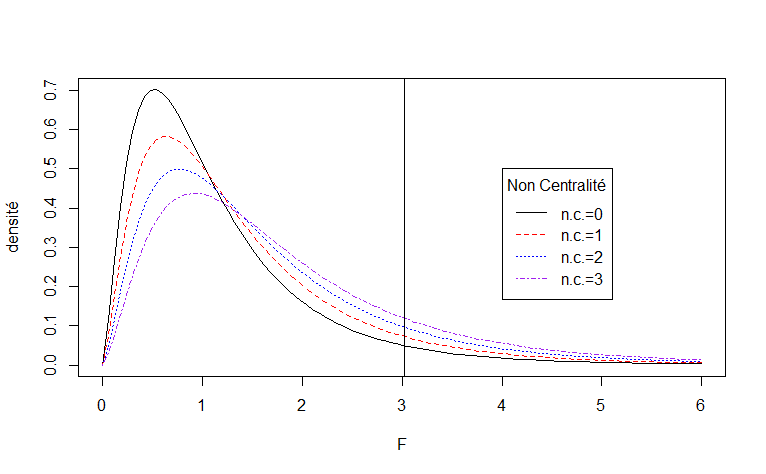
curve(df(x,5,13,0),0,6,lty=1,ylab="densité",xlab="F")
curve(df(x,5,13,1),0,6,lty=2,add=TRUE,col="red")
curve(df(x,5,13,2),0,6,lty=3,add=TRUE,col="blue")
curve(df(x,5,13,3),0,6,lty=4,add=TRUE,col="purple")
abline(v=qf(0.95,5,13))
legend(4, 0.5, legend=c("n.c.=0","n.c.=1","n.c.=2","n.c.=3"),
col=c("black","red", "blue","purple"), lty=1:4,
title="Non Centralité")
Calcul de puissance: La puissance d'un test est définie comme étant la probabilité de rejetter H0. Quand H0 est vraie, la puissance est P(rejet H0|H0 est vraie)=α. Mais, si Ha est vraie la puissance sera un fonction de la taille de l'échantillon et de la taille de l'effet. Dans le cas du test linéaire générale, la puissance est une fonction du paramètre de non-centralité λ=nf2, où f2 est le f2 de Cohen. La puissance du test linéaire générale est
puissance=P(F(p−q,n−p,λ=nf2)>F(0,95;p−q,n−p)).
Ecrivons notre propre fonction qui calcul la puissance avec R.
power.partiel.F <- function(p,q,n,f2,alpha)
{
1-pf(qf(1-alpha,p-q,n-p),p-q,n-p,n*f2)
}
Exemple: Considérons un test linéaire générale avec p=7, q=2 et n=20. Calculons la puissance pour (a) f2=0,1; (b) f2=2,5.
(a) La puissance est
puissance=P(F(p−q=5,n−p=13,λ=nf2=2)>F(0,95;p−q=5,n−p=13))=P(F(5,13,2)>3.025438)=0.1194.
> qf(0.95,5,13)
[1] 3.025438
> power.partiel.F(p=7,q=2,n=20,f2=0.1,alpha=0.05)
[1] 0.119406
(b) La puissance est
puissance=P(F(p−q=5,n−p=13,λ=nf2=50)>F(0,95;p−q=5,n−p=13))=P(F(5,13,50)>3.025438)=0.9975.
]
> power.partiel.F(p=7,q=2,n=20,f2=2.5,alpha=0.05)
[1] 0.9975355
Calcul d'une taille d'échantillon: (a) Nous voulons planifier une étude. Nous allons utiliser un test linéaire générale avec p=7, q=2. Nous voulons déterminer la taille de l'échantillon n adéquate afin d'identifier
une taille de l'effet de f2=1,5 avec une puissance de 80\% \`a un niveau de signification de α=5%.
Puisque n>p, alors nous allons évaluer la puissance du test à n=8,8,9,10, et ainsi de suite jusqu\'a ce que nous avons une puissance de 80%. On observe que la taille de l'échantillon requise est n=16 et la puissance correspondante est 81,88%.
> p<-7; q<-2; alpha<-0.05; f2<-1.5
> n<-p
> power<-0
> while (power <0.8)
+ {
+ n<-n+1
+ power<-power.partiel.F(p,q,n,f2,alpha)
+ }
> power
[1] 0.8187186
> n
[1] 16
(b) Vérifions qu'à n=15, la puisance sera plus petite que 80%. La puissance à n=15, si f2=2,5, est
puissance=P(F(p−q=5,n−p=15−7=8,λ=nf2=(15)(1,5)=22,5)>F(0,95;p−q=5,n−p=8))=P(F(5,8,22,5)>3,687499)=0.7594.
> qf(0.95,5,8)
[1] 3.687499
> power.partiel.F(p=7,q=2,n=15,f2=1.5,alpha=0.05)
[1] 0.7593985
Exemple 23 : Comparer des modèles emboités pour tester des hypothèses (Test F partiel)
Considérons un modèle linéaire avec la matrice du plan X de taille n×p. Supposons que nous voulons tester H0 qui nous donne un modèle réduit qui est emboité dans notre modèle. Supposons que X0 de taille n×q est la matrice du plan du
modèle réduit, où les colonnes de X0 appartiennent à l'espace colonne de X. On peut tester H0 avec la statistique F suivante:
F∗=ExtraSS/(p−q)SSE/(n−p), où ExtraSS=SSE(R)−SSE.
Plus que ExtraSS est grande, plus que nous avons des preuves contre H0. Sous H0, la statistique suit une loi F(p−q,n−p). Alors, la valeur-p est P(F(p−q,n−p)>F∗), où F∗ est la valeur observ\'ee de la statistique.
Exemple [Rétablissement]: Considérons les données d'une étude observationnelle bio-médicale. Les participants de cette étude
dans une étude a subi une opération du genou. La variable dépendante est le temps de rééducation, et la variable explicative est une variable catégorique décrivant la forme du patient avant une intervention chirurgicale (1 = inférieur à la moyenne; 2 = moyen; 3 = supérieur à la moyenne). Les 24 participants sont des hommes de 18 ans à 30 ans. Nous avons aussi l'âge du participant dans le jeu de données.
Les données sont dans le fichier : genou.csv. On importe les données et on affiche quelques rangés du jeu de données. On change type du vecteur \verb|genou| en vecteur catégorique et on affiche ces niveaux.
> genou<-read.csv("genou.csv")
> head(genou)
Temps Groupe Age
1 29 1 18.3
2 42 1 30.0
3 38 1 26.5
4 40 1 28.1
5 43 1 29.7
6 40 1 27.8
> genou$Groupe<-factor(genou$Groupe)
> levels(genou$Groupe)
[1] "1" "2" "3"
On veut décrire le temps de rétablissement selon la forme, mais en ajustant l'âge. On commence par tester qu'il n'y pas d'interactions entre l'âge et la forme.
Nous allons ajuster le modèle linéaire suivant:
E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age)+β4(Age)I{Groupe=2}+β5(Age)I{Groupe=3}.
Nous voulons tester l'hypothèse nulle qu'il n'y a pas d'interactions entre la forme et l'âge.
H0 : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age)
contre
Ha : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age)+β4(Age)I{Groupe=2}+β5(Age)I{Groupe=3}.
On ajuste les deux modèles et on les compare avec la fonction anova. N.B. En imposant les contraintes de H0, on a perdu deux paramètres. Alors, le nombre de degrés de liberté du numérateur est 2.
> mod<-lm(formula = Temps ~ Groupe + Age+Groupe*Age, data = genou)
> mod<-lm(formula = Temps ~ Groupe + Age+Groupe*Age, data = genou)
> mod0<-lm(formula = Temps ~ Groupe + Age, data = genou)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: Temps ~ Groupe + Age
Model 2: Temps ~ Groupe + Age + Groupe * Age
Res.Df RSS Df Sum of Sq F Pr(>F)
1 20 6.1657
2 18 5.9439 2 0.22184 0.3359 0.7191
La statistique du test est
F∗=ExtraSS/(p−q)SSE/(n−p)=0,22184/25,9439/18=0.3359.
La valeur-p=P(F(2,18)>0.3359)=0.7191)$. Les preuves qu'il y ait des interactions entre l'âge et la forme ne sont pas significatives.
Signification des variables explicatives d'un modèle additif: Nous allons utiliser un modèle linéaire additif pour décrire le lien entre le temps de rétablissements et les variables explicatives qui sont la forme pré-opération et l'âge.
La fonction de la moyenne du modèle est
E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age).
- Test pour la signification de l'âge: On veut tester H0:β3=0 contre Ha:β3≠0. On peut utiliser un statistique t ou F pour tester ces hypothèses.
Avec une statistique t~: La valeur observée de la statistique est t∗=b3/s{b3}=36,4608. La valeur-p est 2P(T(20)>36,4608)=9,1×10−20. L'âge est une variable explicative significative du temps de rétablissement.
> mod<-lm(formula = Temps ~ Groupe + Age, data = genou)
> summary(mod)$coeff
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.431688 0.86106382 8.630821 3.538937e-08
Groupe2 -1.847379 0.28694289 -6.438141 2.802274e-06
Groupe3 -8.722893 0.33296397 -26.197708 5.914908e-17
Age 1.167286 0.03201483 36.460804 9.075467e-20
> mod$df.residual
[1] 20
Avec une statistique F~: On veut tester
H0 : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3} contre Ha : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age).
La statistique du test est
F∗=ExtraSS/(p−q)SSE/(n−p)=1329,4.
La valeur-p du test est P(F(1,20)>1329,4)=2,2×10−16.
> mod<-lm(formula = Temps ~ Groupe + Age, data = genou)
> mod0<-lm(formula = Temps ~ Groupe , data = genou)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: Temps ~ Groupe
Model 2: Temps ~ Groupe + Age
Res.Df RSS Df Sum of Sq F Pr(>F)
1 21 416.00
2 20 6.17 1 409.83 1329.4 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Remarque: Les deux tests sont équivalents. On peut démontrer que (t∗)2=F∗.
- Test pour la signification de la forme pré-opération~: La fonction de la moyenne du modèle est
E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age).
On veut tester
H0:β1=0,β2=0 contre Ha:H0 est fausse.
Ici on ne peut pas utiliser un test t. Mais, on peut utiliser un test F. On veut tester
H0 : E{Y}=β0+β3(Age) contre Ha : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age).
La statistique du test est
F∗=ExtraSS/(p−q)SSE/(n−p)=399,11.
La valeur-p du test est P(F(2,20)>399,11)=2,2×10−16. La forme pré-opération est une variable explicative significative.
> mod<-lm(formula = Temps ~ Groupe + Age, data = genou)
> mod0<-lm(formula = Temps ~ Age, data = genou)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: Temps ~ Age
Model 2: Temps ~ Groupe + Age
Res.Df RSS Df Sum of Sq F Pr(>F)
1 22 252.249
2 20 6.166 2 246.08 399.11 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Obtenir la signification de toutes les variables explicatives d'un modèle: On peut utiliser la fonction anova, mais c'est pas exactement ce que nous allons vouloir. Ensuite, nous allons vous montrer la fonction drop1 et la fonction Anova du package car.
- La fonction
anova sur un seul objet lm nous donne des tests séquentielles. Remarquer que si Age est la deuxième variable explicative, alors son F∗ est 1329. Tandis que si Age est la première variable explicative, son F∗
est 399. Lequel est correct?
> mod<-lm(formula = Temps ~ Groupe + Age, data = genou)
> anova(mod)
Analysis of Variance Table
Response: Temps
Df Sum Sq Mean Sq F value Pr(>F)
Groupe 2 672.00 336.00 1089.9 < 2.2e-16 ***
Age 1 409.83 409.83 1329.4 < 2.2e-16 ***
Residuals 20 6.17 0.31
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> mod<-lm(formula = Temps ~ Age+Groupe, data = genou)
> anova(mod)
Analysis of Variance Table
Response: Temps
Df Sum Sq Mean Sq F value Pr(>F)
Age 1 835.75 835.75 2710.95 < 2.2e-16 ***
Groupe 2 246.08 123.04 399.11 < 2.2e-16 ***
Residuals 20 6.17 0.31
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Si on utilise Temps ~ Groupe + Age, alors les hypothèses pour Groupe sont
H0 : E{Y}=β0 contre Ha : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}.
et les hypothèses pour Age sont
H0 : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}. contre Ha : E{Y}=β0+β1I{Groupe=2}+β2I{Groupe=3}+β3(Age).
Alors, seulement le test pour Age est correct, dans le sense qu'on ajuste pour Groupe.
Si on utilise Temps ~ Age + Groupe, alors les hypothèses pour Age sont
H0 : E{Y}=β0. contre Ha : E{Y}=β0+β1(Age).
et les hypothèses pour Groupe sont
H0 : E{Y}=β0+β1(Age). contre Ha : E{Y}=β0+β1(Age)+β2I{Groupe=2}+β3I{Groupe=3}.
Alors, seulement le test pour Groupe est correct, dans le sense qu'on ajuste pour Age.
- Avec la fonction
drop1, on peut tester pour la signification de chacune des variables explicatives en ajustant pour les autres variables dans le modèle.
> mod<-lm(formula = Temps ~ Groupe + Age, data = genou)
> drop1(mod, test="F")
Single term deletions
Model:
Temps ~ Groupe + Age
Df Sum of Sq RSS AIC F value Pr(>F)
6.17 -24.617
Groupe 2 246.08 252.25 60.457 399.11 < 2.2e-16 ***
Age 1 409.83 416.00 74.463 1329.39 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Exemple 24 : Test de la signification de la régression
Considérons un modèle linéaire avec la fonction de la moyenne suivante
E{Y}=β0+β1x1+…+βp−1xp−1.
Une façon de décrire la valeur explicative du modèle est de vérifier que le modèle est significatif, dans le sense qu'il y a au moins une variable explicative significative.
Le test de la signification de la régression est de confronter
H0 : βj=0, pour j=1,2,…,p−1 contre Ha : βj≠0, pour au moins un j .
La statistique du test est
F∗=MSRMSE=SSR/(p−1)SSE/(n−p),
qui suit une loi F(p−1,n−p) si H0 est vraie. Des grandes valeurs de F∗ sont considéré comme des preuves contre H0.
Exemple [Dwayne Studios]: Nous allons considérer les données dans le fichier Dwayne.csv. Dwayne studios est une compagnie qui a des studios dans n=21 villes de taille moyenne. Leur spécialité est la photographie des enfants. Les variables sont des descriptions des studios dans chacune de ces villes. Elles sont les ventes y, le nombre d'enfants d'\^ages 16 ou moins dans la communaut\'e x1, et
le revenu disponible par habitant x2 (en milliers de dollars).
Le mod\`ele de r\'egression estim\'ee est
y^=−68,8571+0,00145x1+9,3655x2.
> dwayne<-read.csv("Dwayne.csv")
> head(dwayne)
sales num.children disposible.income
1 174.4 68500 16.7
2 164.4 45200 16.8
3 244.2 91300 18.2
4 154.6 47800 16.3
5 181.6 46900 17.3
6 207.5 66100 18.2
> mod<-lm(sales~num.children+disposible.income,data=dwayne)
> coefficients(mod)
(Intercept) num.children disposible.income
-68.85707315 0.00145456 9.36550038
Est-ce qu'on peut utiliser x1 et x2 pour pr\'evoir les ventes dans une autre communit\'e? En d'autres-mots, est-ce que la régression est significative?
On veut tester H0:β1=β2=0 contre Ha: au moins un des coefficients β1,β2 n'est pas zéro.
La statistique du test est
F∗=SSR/(p−1)SSE/(n−p)=99,1
et la valeur-p est P(F(2,18)>99,1)=1,921×10−10. La régression est significative.
> summary(mod)
Call:
lm(formula = sales ~ num.children + disposible.income, data = dwayne)
Residuals:
Min 1Q Median 3Q Max
-18.4239 -6.2161 0.7449 9.4356 20.2151
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6.886e+01 6.002e+01 -1.147 0.2663
num.children 1.455e-03 2.118e-04 6.868 2e-06 ***
disposible.income 9.366e+00 4.064e+00 2.305 0.0333 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 11.01 on 18 degrees of freedom
Multiple R-squared: 0.9167, Adjusted R-squared: 0.9075
F-statistic: 99.1 on 2 and 18 DF, p-value: 1.921e-10
Tester pour la signication de la régression avec le test linéaire général: On veut tester H0:β1=β2=0. Ceci est équivalent à confronter
H0:E{Y}=β0 contre Ha:E{Y}=β0+β1x1+β2x2.
Nous ajustons les deux modèles et on les compare avec la fonction anova. La statistique du test est
F∗=Extra/(p−q)SSE/(n−p)=99,103,
et la valeur-p est P(F(2,18)>99,103)=1,92×10−10.
> mod<-lm(sales~num.children+disposible.income,data=dwayne)
> mod0<-lm(sales~1,data=dwayne)
> anova(mod0,mod)
Analysis of Variance Table
Model 1: sales ~ 1
Model 2: sales ~ num.children + disposible.income
Res.Df RSS Df Sum of Sq F Pr(>F)
1 20 26196.2
2 18 2180.9 2 24015 99.103 1.921e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Commentaires: Les deux approches pour le test de la signification de la régression sont équivalentes.
Exemple 25 : La loi F non-centrée
Considérons un test linéaire général avec p=7, q=2 et n=20. La statistique du test F∗ suit une loi F(p−q=5,n−p=13,λ),
o\`u
λ=E{Y}′(H−H0)E{Y}σ2=nf2,
et H est la matrice chapeau du mod\`ele complet et H0 est la matrice chapeau du mod\`ele r\'eduit, et f2 est le f2 de Cohen.
Voici un graphe de la densité de probabilité de la loi F(p−q=5,n−p=13,λ), pour λ=0, λ=1,\lambda=2,et\lambda=3.NousavonsaussisuperimposéunedroiteverticaleàlavaleurcritiqueF(0,\!95;5,13).Rappel:OnrejetteH_0siF^*>F(0,\!95;5,13).Plusque\lambda=n\,f^2estgrand,plusquechancederejetterH_0$ augmente.

curve(df(x,5,13,0),0,6,lty=1,ylab="densité",xlab="F")
curve(df(x,5,13,1),0,6,lty=2,add=TRUE,col="red")
curve(df(x,5,13,2),0,6,lty=3,add=TRUE,col="blue")
curve(df(x,5,13,3),0,6,lty=4,add=TRUE,col="purple")
abline(v=qf(0.95,5,13))
legend(4, 0.5, legend=c("n.c.=0","n.c.=1","n.c.=2","n.c.=3"),
col=c("black","red", "blue","purple"), lty=1:4,
title="Non Centralité")
Calcul de puissance: La puissance d'un test est définie comme étant la probabilité de rejetter H0. Quand H0 est vraie, la puissance est P(rejet H0|H0 est vraie)=α. Mais, si Ha est vraie la puissance sera un fonction de la taille de l'échantillon et de la taille de l'effet. Dans le cas du test linéaire générale, la puissance est une fonction du paramètre de non-centralité λ=nf2, où f2 est le f2 de Cohen. La puissance du test linéaire générale est
puissance=P(F(p−q,n−p,λ=nf2)>F(0,95;p−q,n−p)).
Ecrivons notre propre fonction qui calcul la puissance avec R.
power.partiel.F <- function(p,q,n,f2,alpha)
{
1-pf(qf(1-alpha,p-q,n-p),p-q,n-p,n*f2)
}
Exemple: Considérons un test linéaire générale avec p=7, q=2 et n=20. Calculons la puissance pour (a) f2=0,1; (b) f2=2,5.
(a) La puissance est
puissance=P(F(p−q=5,n−p=13,λ=nf2=2)>F(0,95;p−q=5,n−p=13))=P(F(5,13,2)>3.025438)=0.1194.
> qf(0.95,5,13)
[1] 3.025438
> power.partiel.F(p=7,q=2,n=20,f2=0.1,alpha=0.05)
[1] 0.119406
(b) La puissance est
puissance=P(F(p−q=5,n−p=13,λ=nf2=50)>F(0,95;p−q=5,n−p=13))=P(F(5,13,50)>3.025438)=0.9975.
]
> power.partiel.F(p=7,q=2,n=20,f2=2.5,alpha=0.05)
[1] 0.9975355
Calcul d'une taille d'échantillon: (a) Nous voulons planifier une étude. Nous allons utiliser un test linéaire générale avec p=7, q=2. Nous voulons déterminer la taille de l'échantillon n adéquate afin d'identifier
une taille de l'effet de f2=1,5 avec une puissance de 80\% \`a un niveau de signification de α=5%.
Puisque n>p, alors nous allons évaluer la puissance du test à n=8,8,9,10, et ainsi de suite jusqu\'a ce que nous avons une puissance de 80%. On observe que la taille de l'échantillon requise est n=16 et la puissance correspondante est 81,88%.
> p<-7; q<-2; alpha<-0.05; f2<-1.5
> n<-p
> power<-0
> while (power <0.8)
+ {
+ n<-n+1
+ power<-power.partiel.F(p,q,n,f2,alpha)
+ }
> power
[1] 0.8187186
> n
[1] 16
(b) Vérifions qu'à n=15, la puisance sera plus petite que 80%. La puissance à n=15, si f2=2,5, est
puissance=P(F(p−q=5,n−p=15−7=8,λ=nf2=(15)(1,5)=22,5)>F(0,95;p−q=5,n−p=8))=P(F(5,8,22,5)>3,687499)=0.7594.
> qf(0.95,5,8)
[1] 3.687499
> power.partiel.F(p=7,q=2,n=15,f2=1.5,alpha=0.05)
[1] 0.7593985
Exemple 31 : La régression polynomiale
La motivation de la régression polynomiale:
- Considérons un modèle simple (c'est-à-dire un prédicteur), où le lien entre \(y\) et \(x\) est complexe et non linéaire. En supposant que le lien fonctionnelle est lisse, alors du Thèorème de Taylor de vos cours de calcul, on sait qu'on peut approximer la fonction par un polyn\^ome. Quand nous utilisons la fonction de la moyenne
\[
E\{Y\}=\beta_0+\beta_1\,x,
\]
On dit que nous utilisons un modèle linéaire d'ordre 1. En d'autres-mots, nous ne supposons pas nécessairement que le lien est exactement linéaire, mais plutôt que la fonction linéaire en $x$ sera une bonne approximation du vrai lien fonctionnelle entre \(y\) et \(x\).
- En outre, le Théorème de Taylor nous dit qu'en augmentant l'ordre du polynôme, on aura une meilleure approximation. Nous pourrions approximer le lien fonctionnelle entre \(y\) et \(x\) avec une fonction de la moyenne quadratique ou cubique en \(x\). Voici une fonction de la moyenne d'ordre 3 :
\[
E\{Y\}=\beta_0+\beta_1\,x+\beta_2\,x^2+\beta_3\,x^3.
\]
Ceci un modèle linéaire, où \(x_1=x\), \(x_2=x^2\), et \(x_3=x^3\).
Exemple [Stéroïdes dans le plasma]: Le nuage de points ci-dessous présente des données sur l'âge et le niveau d'un stéroïde dans le plasma pour 27 femmes en bonne santé entre 8 et 25 ans. Les données suggèrent fortement que le lien statistique entre \(y\) et \(x\) est non-linéaire. Les données sont dans le fichier : Steroid-Plasma.csv
Nous importons les données et nous affichons la structure du jeu de données. En outre, nous produisons le nuage de points avec une superposition d'une courbe lisse. La courbe lisse suggère que, à mesure que l'âge augmente, le niveau de stéroïdes augmente jusqu'à un certain point, puis commence à diminuer légèrement. Nous allons essayer de modéliser le lien entre ces \(y\) et \(x\) avec un modèle linéaire d'ordre 3 en \(x\).
> plasma<-read.csv("Steroid-Plasma.csv")
> str(plasma)
'data.frame': 27 obs. of 2 variables:
$ Age..in.years.: int 8 8 9 9 9 10 11 12 12 13 ...
$ Steroid.Level : int 2 5 3 9 12 10 15 10 19 11 ...
with(plasma,scatter.smooth(Steroid.Level~Age..in.years.,
xlab="Age en années",ylab="Stéroïdes dans le plasma"))
Application 1: Nous allons utiliser la régression polynomiale comme une diagnostique du modèle linéaire. Une des conditions sous-jacente d'un modèle linéaire est que la fonction de la moyenne est bien spécifiée. Pour la plupart des applications où nous décrivons la distribution de \(y\) selon \(x\), nous souposons que
\[
E\{Y\}=\beta_0+\beta_1\,x.
\]
Si la fonction de la moyenne n'est pas bien spécifiée, c'est-à-dire que le lien statistique n'est pas approximativement linéaire, alors nous allons devrions être capable d'identifier des effets d'ordres supérieures.
Nous allons ajuster un modèle linéaire d'ordre 3 pour décrire le niveau du stéroïde dans le plasma selon l'âge. Notre but est d'identifier des effets significatifs d'ordre 2 ou 3.
> mod<-lm(Steroid.Level~Age..in.years.+I(Age..in.years.^2)+I(Age..in.years.^3), data=plasma)
Ensuite, nous allons utiliser des test séquentiels (aussi dit de type I) pour vérifier la signification des différents types d'effets. On obtient les tests séquentiels avec la fonction anova().
> anova(mod)
Analysis of Variance Table
Response: Steroid.Level
Df Sum Sq Mean Sq F value Pr(>F)
Age..in.years. 1 632.21 632.21 71.7222 1.592e-08 ***
I(Age..in.years.^2) 1 251.70 251.70 28.5542 1.997e-05 ***
I(Age..in.years.^3) 1 12.99 12.99 1.4731 0.2372
Residuals 23 202.74 8.81
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Commentaires:
- On commence toujours avec le test pour la signification de l'effet d'ordre supérieure. Ici c'est les effets cubiques. Le test confrote
\[
H_0:~~E\{Y\}=\beta_0+\beta_1\,x+\beta_2\,x^2
~~ \mbox{ contre } ~~
H_a:~~E\{Y\}=\beta_0+\beta_1\,x+\beta_2\,x^2+\beta_3\,x^3.
\]
Les effets cubiques ne sont pas significatifs (F(1,23)=1,4731; p=0,2373).
- Ensuite, si le effets cubiques ne sont pas significatifs, on passe au test de la signification des effets quadratiques. Le test confrote
\[
H_0:~~E\{Y\}=\beta_0+\beta_1\,x
~~ \mbox{ contre } ~~
H_a:~~E\{Y\}=\beta_0+\beta_1\,x+\beta_2\,x^2.
\]
Les effets quadratiques sont significatifs \((F(1,23)=28,\!554; p<0,\!0001)\).
Nous avons des preuves significatives contre la linéarité du lien statistique entre le niveau du stéroïde dans le plasma et l'âge. La fonction de la moyenne qui est linéaire en l'âge n'est pas bien spécifiée.
- Si les effets quadratiques n'étaient pas significatifs, alors on pourrait passer au test de la signification des effets linéaires.
Le test confrote
\[
H_0:~~E\{Y\}=\beta_0
~~ \mbox{ contre } ~~
H_a:~~E\{Y\}=\beta_0+\beta_1\,x.
\]
Les effets linéaires sont significatifs \((F(1,23)=71,\!7222; p<0,\!0001)\). Mais, ce test est difficile à interpreter dans cet exemple, puisqu'il y a des effets quadratiques.
Application 2: Nous allons utiliser la régression polynomiale comme une mesure corrective de la non-linéarité.
Nous ajustons un modèle linéaire d'ordre deux en l'âge du participant pour décrire la distribution du niveau du stéroïde dans le plasma. La fonction de la moyenne estimée est
\[
\hat{Y}=-25,\!49475+4,\!75598\,x-0,\!11810\,x^2.
\]
Le modèle linéaire d'ordre deux est significatif (F(2,24)=49,17; p<0,0001); \(R^2=0,\!8038\), et l'écart type résiduel est \(s_e=2,998\).
> mod<-lm(Steroid.Level~Age..in.years.+I(Age..in.years.^2),data=plasma)
> summary(mod)
Call:
lm(formula = Steroid.Level ~ Age..in.years. + I(Age..in.years.^2),
data = plasma)
Residuals:
Min 1Q Median 3Q Max
-5.3742 -1.6335 0.0053 1.6777 5.0585
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -25.49475 5.59317 -4.558 0.000128 ***
Age..in.years. 4.75598 0.73714 6.452 1.13e-06 ***
I(Age..in.years.^2) -0.11810 0.02232 -5.292 1.99e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.998 on 24 degrees of freedom
Multiple R-squared: 0.8038, Adjusted R-squared: 0.7875
F-statistic: 49.17 on 2 and 24 DF, p-value: 3.249e-09
Voici un nuage de points du niveau du stéroïde dans le plasma contre l'âge avec un superposition de la fonction de la moyenne estimée.
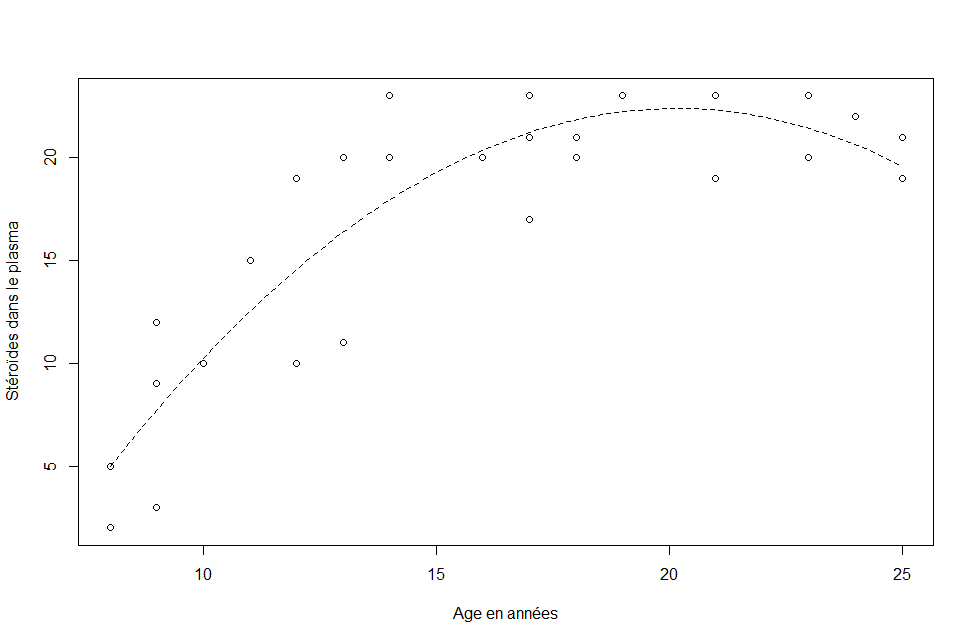
Voici les commandes que nous avons utilisé pour produire ce diagramme.
with(plasma,plot(Steroid.Level~Age..in.years.,
xlab="Age en années",ylab="Stéroïdes dans le plasma"))
mod<-lm(Steroid.Level~Age..in.years.+I(Age..in.years.^2),data=plasma)
xlim<-range(plasma$Age..in.years.)
x<-seq(xlim[1],xlim[2],length.out=100)
newdata<-data.frame(Age..in.years.=x)
y<-predict(mod,newdata)
lines(x,y,type="l",lty=2)
Interpréter les coefficients:
- Le taux de changement (estimé) du niveau moyen du stéroïdes dans le plasma par rapport à l'âge est
\[
\frac{d\hat{\mu}_Y}{dx}=b_1+2\,b_2\,x=4,\!75598-2(0,\!11810)\,x=4,\!75598-0,2363\,x.
\]
- Un coefficient négatif pour le terme quadratique signifie que le taux de changement diminue avec l'âge. Le taux de changement diminue de 0,2363 unité par an.
- \(b_1=4.75598\) est le taux de changement à x=0. Ceci n'a souvent pas un sens dans le context du problème. Par exemple, on ne peut pas imaginer un participant qui a un âge de 0. Pour obtenir un coefficient qui est plus signifiant, on peut centrer le prédicteur autour de sa moyenne. Voici le modèle:
\[
E\{Y\}=\beta_0^*+\beta_1^*(x-\bar{x})+\beta_3^*\,(x-\bar{x})^2.
\]
Le taux de changement (estimé) du niveau moyen du stéroïdes dans le plasma par rapport à l'âge est
\[
\frac{d\hat{\mu}_Y}{dx}= b_1^*+2\,b_2^*\,(x-\bar{x})=1,\!02929-2(0,\!11810)(X-15,\!77778).
\]
\(b_1^*=1,\!029\) signifie que le taux de changement du stéroïde dans le plasma est de 1,029 unité / an pour une participante de 15,8 ans.
> x<-plasma$Age..in.years.
> plasma$Age.c<-x-mean(x)
> mod<-lm(Steroid.Level~Age.c+I(Age.c^2),data=plasma)
> summary(mod)
Call:
lm(formula = Steroid.Level ~ Age.c + I(Age.c^2), data = plasma)
Residuals:
Min 1Q Median 3Q Max
-5.3742 -1.6335 0.0053 1.6777 5.0585
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.14462 0.86933 23.173 < 2e-16 ***
Age.c 1.02929 0.10980 9.374 1.71e-09 ***
I(Age.c^2) -0.11810 0.02232 -5.292 1.99e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.998 on 24 degrees of freedom
Multiple R-squared: 0.8038, Adjusted R-squared: 0.7875
F-statistic: 49.17 on 2 and 24 DF, p-value: 3.249e-09
> mean(x)
[1] 15.77778
- La fonction de la moyenne quadratique estimée avec le prédicteur centré autour de sa moyenne est
\[
\hat{Y}=20,\!14462+1,\!02929\,(X-15,\!77778)-0,\!11810\,(X-15,\!77778)^2.
\]
- Nous n'avons pas besoin de centrer autour de la moyenne. On peut centrer autour d'une valeur plus simple à décrire qui est proche de la moyenne. Par ex. un âge de 16 ans.
\[
\hat{Y} = 20,\!14462 + 0,\!9768\,(X - 16) - 0,\!11810\,(X - 16)^2.
\]
> plasma$Age.c<-plasma$Age..in.years.-16
> model<-lm(Steroid.Level~Age.c+I(Age.c^2),data=plasma)
> summary(model)
Call:
lm(formula = Steroid.Level ~ Age.c + I(Age.c^2), data = plasma)
Residuals:
Min 1Q Median 3Q Max
-5.3742 -1.6335 0.0053 1.6777 5.0585
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.36752 0.87300 23.330 < 2e-16 ***
Age.c 0.97680 0.10797 9.047 3.34e-09 ***
I(Age.c^2) -0.11810 0.02232 -5.292 1.99e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.998 on 24 degrees of freedom
Multiple R-squared: 0.8038, Adjusted R-squared: 0.7875
F-statistic: 49.17 on 2 and 24 DF, p-value: 3.249e-09
> confint(model)
2.5 % 97.5 %
(Intercept) 18.5657335 22.16930805
Age.c 0.7539739 1.19963235
I(Age.c^2) -0.1641610 -0.07203762
> confint(model)[3,]*2
2.5 % 97.5 %
-0.3283219 -0.1440752
Interprétation: Nous estimons que pour une femme en bonne santé de 16 ans, le niveau de stéroïdes dans le plasma se situe entre 18,6 et 22,2 unités. Le taux de changement dans le niveau du stéroïde par rapport à l'âge est compris entre 0,75 unité / an et 1,20 unité / an pour une femme en bonne santé de 16 ans. Nous estimons que le taux de changement diminue de 0,14 à 0,32 unité / an.
Commentaires: Il est bon de donner dans la section des commentaires de l'analyse quelques intervalles de confiance pour \(E \{Y\}\) pour quelques valeurs différentes de $x$ dans le cadre de l'étude, en particulier lorsque le lien n'est pas linéaire.
Exemple 32 : Une spline linéaire
Une alternative à la régression polynomiale est la régression avec une spline linéaire, c'est-à-dire une fonction de la moyenne qui est linéaire par morceau.
Exemple 33 : Interactions entre prédicteurs
Lors de l'utilisation d'un modèle linéaire d'ordre 1 en $x_1,x_2,\cdots,x_{p-1}$ tel que
\[
E\{Y\} = \beta_0+\beta_1\,x_1+\ldots+\beta_{p-1}\,x_{p-1},
\]
on dit que les effets des prédicteurs sont additifs. Pour un modèle additif, nous n'avons pas besoin de considérer les valeurs des autres prédicteurs pour décrire le lien partiel entre \(Y\) et le prédicteur \(x_j\). Par exemple, le taux de variation de \(E\{Y\}\) par rapport à $x_j$ est
\[
\frac{\partial E\{Y\} }{\partial x_j}=\beta_j ~~ (\mbox{qui ne dépend pas de la valeur des autres prédicteurs}).
\]
Cependant, nous pouvons imaginer un scénario où une association partielle entre Y et un prédicteur peut varier en fonction de la valeur d'une autre variable. Pensez à l'effet de la consommation d'alcool sur des drogues particulières. La consommation d'alcool peut rendre certains médicaments inefficaces ou, pire encore, produire des effets secondaires indésirables. Nous dirions que la drogue et l'alcool interagissent.
Une façon d'approximer l'interaction entre les prédicteurs consiste à inclure des termes bilinéaires dans le modèle (ce sont des termes d'ordre 2).
Voici un exemple de modèle linéaire avec des termes d'interaction d'ordre 2 :
\[
E\{Y\}= \beta_0 + \beta_1\,x_1 + \beta_2\,x2 + \beta_3\,x_1\,x_2.
\]
Pour décrire l'association partielle entre y et chacun des prédicteurs, nous pouvons décrire les taux de changement de à(E\{Y\}\) par rapport à \(x_1\) et par rapport à \(x_2\). Ils sont
\[
\frac{\partial E\{Y\} }{\partial x_1}=\beta_1+\beta_3\,x_2 ~~ (\mbox{qui dépend de la valeur de \(x_2\)})
\]
et
\[
\frac{\partial E\{Y\} }{\partial x_2}=\beta_2+\beta_3\,x_1 ~~ (\mbox{qui dépend de la valeur de \(x_1\)}),
\]
respectivement.
Commentaires:
- Quand \(\beta_1\) et \(\beta_2\) ont le même signe (les deux sont positifs ou les deux sont négatifs), alors on dit que
- l'effet d'interaction entre \(x_1\) et \(x_2\) est de type renforcement ou synergique si \(\beta_3\) est du même signe que \(\beta_1\) et \(\beta_2\);
- l'effet d'interaction entre \(x_1\) et \(x_2\) est de type interférentiel ou antagoniste si \(\beta_3\) est de signe différent de que \(\beta_1\) et \(\beta_2\).
- \(\beta_1\) est l'effet principale de \(x_1\) \`a \(x_2=0\). Ceci n'est souvent pas signifiant. Mais, si nous centrons les prédicteurs
\[
E[Y]=\beta_0^*+\beta_1^*(x_1-\bar{x}_1)+\beta_2^*\,(x_2-\bar{x}_2)+\beta_3^*(x_1-\bar{x}_1)(x_2-\bar{x}_2),
\]
alors
\[
\frac{\partial E\{Y\} }{\partial (x_1-\bar{x}_1)}=\beta_1^*+\beta_3^*\,(x_2-\bar{x}_2) ~~ (\mbox{qui dépend de la valeur de \(x_2-\bar{x}_2\)})
\]
et
\[
\frac{\partial E\{Y\} }{\partial (x_2-\bar{x}_2)}=\beta_2^*+\beta_3^*\,(x_1-\bar{x}_1) ~~ (\mbox{qui dépend de la valeur de \(x_1-\bar{x}_1\)}).
\]
Alors \(\beta_1^*\) décrit le taux de variation entre \(E\{Y\}\) par rapport à \(x_1\) à \(x_2=\bar{x}_2\). (N.B. Il n'est pas nécessaire de centrer autour de la moyenne. On peut utiliser une autre valeur qui est motivé par l'application ou une valeur proche de la moyenne).
La syntaxe R pour les interactions entre x1 et x2 est x1:x2. Mais il y a quelques notations abrégées:
Pour ajouter toutes les interactions d'ordre 2 (pour 3 prédicteurs), nous utilisons:
(x1 + x2 + x3) ^ 2
Ce qui précède donne x1 + x2 + x3 + x1:x2 + x1:x3 + x2:x3.
Pour obtenir tous les termes d'interaction, nous utilisons
x1 * x2 * x3
Ce qui précède donne x1 + x2 + x3 + x1:x2 + x1:x3 + x2:x3 + x1:x2:x3.
Nous allons utiliser le jeu de données Boston de la librairie MASS.
# charger la librarie
library(MASS)
# description du jeu de données
? Boston
Nous allons considérer 3 des variables:
- y=medv = valeur médiane des maisons occupées par leur propriétaire en milliers de dollars;
- \(x_1\) = rm = nombre moyen de pièces par logement;
- \(x_2\) = age = proportion de logements occupés par leur propriétaire construits avant 1940;
- \(x_3\) = lstat = proportion de la population de classe inférieure.
Nous ajustons un modèle avec des interactions d'ordre 2 pour décrire medv selon rm, age, et lstat.
> mod<-lm(medv~(rm+age+lstat)^2,data=Boston)
> coefficients(mod)
(Intercept) rm age lstat rm:age rm:lstat age:lstat
-78.71823177 15.97999835 0.65961841 3.06941245 -0.08331668 -0.46956897 -0.01197715
Le modèle estimé est
\[
\hat{y}=-78,\!7182+ 15,\!9800\,x_1+ 0,\!6596\,x_2+3,\!069\,x_3-0,\!0833\,x_1\,x_2 -0,\!4696\,x_1\,x_3 -0,\!0120\,x_2\,x_3.
\]
On utilise un test linéaire général pour tester la signification d'une interaction. La pratique commune est d'utiliser des tests de type II (aussi dit des tests partiels), quand il y a des effets d'ordres supérieurs dans le modèle.
> library(car)
> Anova(mod,type="II")
Anova Table (Type II tests)
Response: medv
Sum Sq Df F value Pr(>F)
rm 3563.5 1 178.3792 < 2.2e-16 ***
age 172.3 1 8.6244 0.00347 **
lstat 5257.7 1 263.1891 < 2.2e-16 ***
rm:age 578.3 1 28.9467 1.146e-07 ***
rm:lstat 3128.3 1 156.5967 < 2.2e-16 ***
age:lstat 893.5 1 44.7278 6.085e-11 ***
Residuals 9968.5 499
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Description d'un test partiel:
- Considérons un effet d'ordre 2, par exemple l'interaction entre rm et age. Quand nos testons pour la signification de cette interaction [\(H_0:\beta_4=0\)], nous ajustons pour tous les autres effets d'ordre 2 ou inférieur. Alors nous testons
\[
H_0 : E\{Y\}=\beta_0+\beta_1\,x_1+\beta_2\,x_2+\beta_3\,x_2+\beta_5\,x_1\,x_3+\beta_6\,x_2\,x_3.
\]
contre
\[
H_a: E\{Y\}=\beta_0+\beta_1\,x_1+\beta_2\,x_2+\beta_3\,x_2+\beta_4\,x_1\,x_2+\beta_5\,x_1\,x_3+\beta_6\,x_2\,x_3.
\]
- Considérons un effet d'ordre 1, par exemple l'effet principal de \(x_1\). Quand nos testons pour la signification de l'effet principal de $x_1$ [\(H_0:\beta_1=0\)], nous ajustons pour tous les autres effets sauf pour les effets d'ordre 2 concernant \(x_1\). Alors nous testons
\[
H_0 : E\{Y\}=\beta_0+\beta_2\,x_2+\beta_3\,x_2+\beta_6\,x_2\,x_3.
\]
contre
\[
H_a: E\{Y\}=\beta_0+\beta_1\,x_1+\beta_2\,x_2+\beta_3\,x_2+\beta_6\,x_2\,x_3.
\]
- Pourquoi est-ce qu'on ignore les effets d'ordre supérieurs à \(x_1\) quand nous testons les effets principaux? En général, c'est difficile à interpréter un effet principal s'il y a des effets d'ordre supérieur. S'il y a des interactions significatifs qui implique \(x_1\), alors on sait qu'il y a des effets significatifs concernant \(x_1\). On peut s'arrêta là, et essayer de décrire ces effets.
Exemple 34 : Test de l'inadéquation de l'ajustement (Test for lack-of-fit)
Exemple [Banque]: Voici un jeu de données: BankExample.csv.
Nous importons les données et nous affichons quelques colonnes.
> head(banque)
min.deposit new.accounts
1 125 160
2 100 112
3 200 124
4 75 28
5 150 152
6 175 156
Commentaires: - Une banque avait des offres différentes aux clients à 12 branches de tailles similaires qui ouvrent un compte du marché monétaire. La banque a imposé des dépots minimum aux différentes branches.
- L'unité statistique est la branche. Pour décrire ces unités on a deux variables : (i) le dépôt minimum qui est imposé à cette branche; (ii) le nombre de nouveaux comptes.
- Nous observons avec une analyse visuelle, que l'association entre le dépôt minimum et le nombre de nouveaux comptes n'est pas linéaire. Nous allons appuyer cette observation avec un test formel dit le test d'inéquation de l'ajustement (aussi dit test for lack-of-fit en anglais).
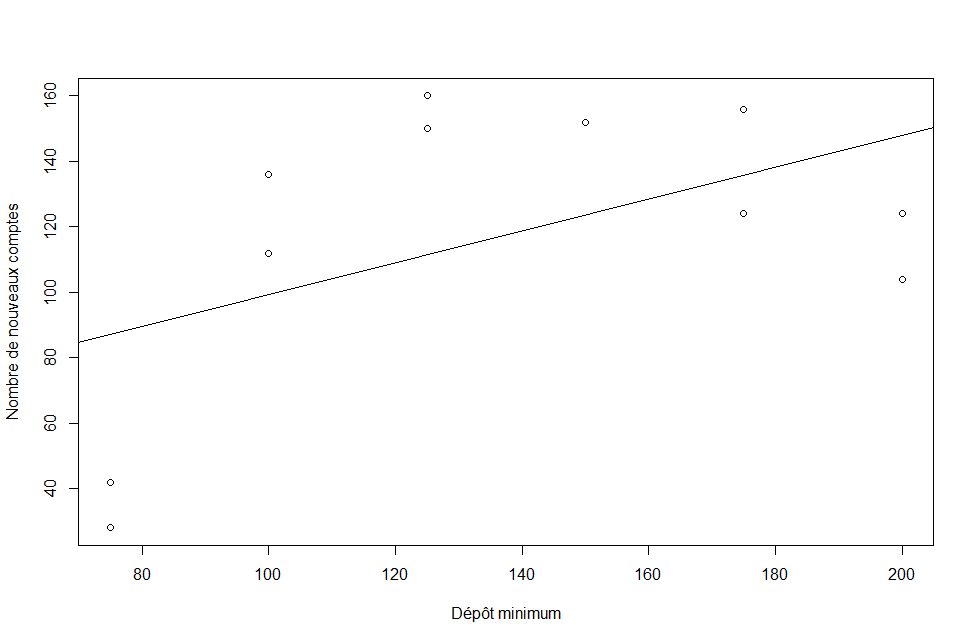
> with(banque,plot(min.deposit,new.accounts,xlab="Dépôt minimum",
+ ylab="Nombre de nouveaux comptes"))
> with(banque,plot(min.deposit,new.accounts,xlab="Dépôt minimum",
+ ylab="Nombre de nouveaux comptes"))
> mod<-lm(new.accounts~min.deposit,data=banque)
> abline(mod)
Test d'inéquation de l'ajustement: Nous voulons tester
\[
H_0:~E\{Y\}=\beta_0+\beta_1\,x ~~~ \mbox{ contre } ~~~ H_a:~E\{Y\}\neq \beta_0+\beta_1\,x.
\]
Pour confronter ces deux hypothèses nous allons emboîté le modèle de régression linéaire simple dans un modèle plus général. Considérer une stratification des unités selon la valeur de \(x\), c'est-à-dire les unités dans le même groupe ont la même valeur de \(x\). Voici un tableau de fréquences pour \(x\)=dépôt minimum. On observe qu'il y a \(c=6\) groupes et que chaque groupe a 2 unités sauf pour le groupe \(x=150\). Ce dernier groupe a seulement 1 unité.
> table(banque$min.deposit)
75 100 125 150 175 200
2 2 2 1 2 2
Nous allons supposé que chaque groupe peut avoir sa propre moyenne. Alors on considère \(x\)=dépôt minimum comme une variable catégorique avec \(c=6\) catégories. Pour indiquer ceci à R, on utilise la fonction factor. Nous allons ajouter une colonne dans le jeu de données (dataframe) banque qui est la variable dépôt minimum, mais elle est une variable catégorique. On affiche aussi les niveaux de cette variable catégorique. Le modèle d'ANOVA correspondant est le modèle le plus complexe possible puisqu'on impose aucune courbe pour \(E\{Y\}\) selon \(x\).
> banque$min.deposit.cat<-factor(banque$min.deposit)
> levels(banque$min.deposit.cat)
[1] "75" "100" "125" "150" "175" "200"
Commentaire: Pour une variable catégorique (a factor en anglais), R va construire des variables muettes (dummy) pour identifier les catégories. Pour afficher ces fonctions, on peut utiliser la fonction contrasts. Ci-bas, chaque colonne est une variable muette. La première identifie la catégorie 100 en donnant 1 seulement si l'unité est dans le groupe "100", sinon c'est 0. Notons que le premier groupe "75" n'a pas de variable muette. Ce groupe est le groupe de référence.
> contrasts(banque$min.deposit.cat)
100 125 150 175 200
75 0 0 0 0 0
100 1 0 0 0 0
125 0 1 0 0 0
150 0 0 1 0 0
175 0 0 0 1 0
200 0 0 0 0 1
Le modèle linéaire (complet) est
\[
Y_i=\beta_0+\beta_1\,x_{i2}+\ldots+\beta_{c-1}\,x_{ic}+\epsilon_i=\left\{
\begin{array}{cc}
\beta_0=\mu_1, & \mbox{l'unité $i$ appartient au groupe 1,} \\
\mu_1+\beta_1=\mu_2 & \mbox{l'unité $i$ appartient au groupe 2,} \\
\mu_1+\beta_2=\mu_3 & \mbox{l'unité $i$ appartient au groupe 3,} \\
\vdots & \vdots \\
\mu_1+\beta_{c-1}=\mu_c & \mbox{l'unité $i$ appartient au groupe c,} \\
\end{array}
\right.
\]
où \(\epsilon_1,\cdots,\epsilon_n\) sont indépendantes \(N(0,\sigma^2)\). N.B.: Ce modèle linéaire est parfois dit un modèle d'ANOVA et le paramètre \(\beta_{j-1}=\mu_j-\mu_1\) est dit l'effet du groupe \(j\) (en comparaison au groupe de référence 1).
Voici un sommaire de l'ajustement du modèle d'ANOVA.
> mod.ANOVA<-lm(new.accounts~min.deposit.cat,data=banque)
> summary(mod.ANOVA)
Call:
lm(formula = new.accounts ~ min.deposit.cat, data = banque)
Residuals:
1 2 3 4 5 6 7 8
5.000e+00 -1.200e+01 1.000e+01 -7.000e+00 -3.331e-15 1.600e+01 7.000e+00 -1.600e+01
9 10 11
-5.000e+00 -1.000e+01 1.200e+01
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.00 10.71 3.267 0.022282 *
min.deposit.cat100 89.00 15.15 5.874 0.002030 **
min.deposit.cat125 120.00 15.15 7.919 0.000517 ***
min.deposit.cat150 117.00 18.56 6.305 0.001478 **
min.deposit.cat175 105.00 15.15 6.930 0.000960 ***
min.deposit.cat200 79.00 15.15 5.214 0.003428 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.15 on 5 degrees of freedom
Multiple R-squared: 0.9423, Adjusted R-squared: 0.8845
F-statistic: 16.32 on 5 and 5 DF, p-value: 0.004085
Le modèle estimé est
\[
\hat{E}\{Y|X=x\}
=\left\{
\begin{array}{cc}
\bar{y}_1=35, & \mbox{ si $x=75$} \\
\bar{y}_2=35+89=124, & \mbox{ si $x=100$} \\
\bar{y}_3=35+120=155, & \mbox{ si $x=125$} \\
\bar{y}_4=35+117=152, & \mbox{ si $x=150$} \\
\bar{y}_5=35+105=140 & \mbox{ si $x=175$} \\
\bar{y}_6=35+79=114, & \mbox{ si $x=200$} \\
\end{array}
\right.
\]
avec l'estimation de la variance (de l'erreur pure) qui est \(s_{\mbox{p.e.}}^2=(15,\!15)^2=229,\!52\). Le coefficient de détermination du modèle d'ANOVA est \(R^2=94,\!23\%\). Mais, le coefficient de détermination du modèle réduit qui est le modèle de régression linéaire simple qui exprime \(y\) en fonction linéaire de \(x\) est \(R^2=25,\!86\%\). L'ajustement des deux modèles sont très différentes. Alors, nous avons des preuves contre le modèle réduit. En d'autres-mots, nous avons des preuves contre la linéarité.
> mod<-lm(new.accounts ~ min.deposit, data=banque)
> summary(mod)$r.squared
[1] 0.2585808
Est-ce que nos preuves contre la linéarité entre \(y\) et \(x\) sont significatives? Nous allons utiliser le test linéaire général pour comparer les deux modèles. La statistique du test est
\[
F=\frac{\mbox{ExtraSS}/(p-q)}{\mbox{MSE}}=\frac{\mbox{SSE}(R)-\mbox{SSE}/(p-q)}{\mbox{MSE}},
\]
o\`u \(p-q\) est la réduction de paramètres par les contraintes de \(H_0\), \(\mbox{SSE}\) et \(\mbox{SSE}(R)\) est la somme de carrés résiduelles du modèle complet et réduit, respectivement. En outre, MSE est l'écart type résiduelle du modèle complet. Nous allons voir en classe que sous \(H_0\) la statistique \(F\) suit une loi \(F(p-q,n-p)\).
Pour le modèle complet nous avons \(c\) paramètres pour décrire la moyenne, tandis que pour le modèle réduit, nous avons \(2\) paramètres pour décrire la moyenne. Alors, \(p-q=c-2\). (Remarquons que nous divisons par \(p-q=c-2\), alors on doit avoir \(c>2\). En d'autres-mots, il nous faut au moins 3 valeurs différentes de \(x\)).
Nous allons voir que la variance résiduelle pour un modèle linéaire avec \(p\) paramètres dans la fonction de la moyenne est \(\mbox{MSE}=\mbox{SSE}/(n-p)\). On peut aussi d\'emontrer que l'estimation par les moindes carr\'es de \(\mu_j\) est \(\hat{\mu}_j=\bar{y}_j\), pour \(j=1,2,\ldots,c\). Alors, pour le modèle complet, on a
\[
\mbox{MSE}=\frac{\sum_{i=1}^n (y_i-\hat{y}_i)^2}{n-p} =\frac{\sum_{i\in A_1} (y_i-\hat{y}_1)^2+\sum_{i\in A_2} (y_i-\hat{y}_2)^2+\cdots+\sum_{i\in A_c} (y_i-\hat{y}_c)^2}{n-p}=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2+\cdots+(n_c-1)s_c^2}{n-c}=s_{p.e.}^2,
\]
où \(A_j\) est le sous-ensembles des indices qui identifie le groupe \(j\). En d'autres-mots, \(\mbox{MSE}\) pour le modèle d'ANOVA est une moyenne pondérée des variances échantillonales des \(c\) groupes. (Remarquons que si le groupe n'a pas au moins deux observations, on aura \(\sum_{i\in A_j} (y_i-\hat{y}_j)^2=0\), puisque la moyenne d'une observation est la valeur de cette observation. Ceci veut dire que si nous n'avons pas un groupe avec au moins deux unités, alors \(\mbox{SSE}=0\) et \(F\) ne peut pas être calculé. Alors, on doit avoir une étude avec des réplications, c'est-à-dire on doit avoir au moins deux unités qui ont la même valeur de \(x\).)
Alors la statistique du test de l'inédaquation de l'ajustement est
\[
F_0=\frac{(\mbox{SSE}(R)-\mbox{SSE})/(c-2)}{s_{p.e.}^2}=\frac{(14742-1148)/(6-2)}{1148/5}=14,\!801.
\]
La valeur \(p\) est \(P(F(4,5)>14,\!801)=0,\!0056\). Les preuves contre la linéarité sont significatives.
> anova(mod,mod.ANOVA)
Analysis of Variance Table
Model 1: new.accounts ~ min.deposit
Model 2: new.accounts ~ min.deposit.cat
Res.Df RSS Df Sum of Sq F Pr(>F)
1 9 14742
2 5 1148 4 13594 14.801 0.005594 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Exemple 35 : Diagnostique pour la spécification de la fonction de la moyenne
Lors de l'évaluation de la pertinence du modèle linéaire, nous devons suivre l'ordre suivant
- Identifier les valeurs aberrantes et les observations influentes;
- Test des erreurs dans la spécification de la fonction de la moyenne;
- Test d'hétéroscédasticité;
- Testez la normalité des erreurs aléatoires.
- Pour (4), nous pouvons utiliser un diagramme quantile-quantile des résidus studentisés.
- Pour (3), nous pouvons utiliser le diagramme d'échelle et localisation pour les résidus studentisés et les tests de Breusch-Pagan et White pour l'hétéroskédasticité.
- Pour (2), nous pouvons le diagramme des résidus contre les valeurs ajustées, et nous pouvons effectuer le test RESET de Ramsey (Regression Equation Specification Error Test). Nous discuterons du test RESET dans cette section.
Le test RESET de Ramsey:
L'idée à Ramsey est simple. Considérons le modèle linéaire:
\[
E\{Y\}=\beta_0+\beta_1\,x_1+\cdots+\beta_{p-1}\,x_{p-1}.
\]
Nous ajustons le modèle, et nous obtenons les valeurs ajustées.
\[
\hat{y}_i=b_0+b_1\,x_1+\cdots+b_{p-1}\,x_{p-1}
\]
pour \(i=1,2,\ldots,n\). Ensuite, on ajoute \(\hat{y}^2\) et \(\hat{y}^2\) comme des prédicteurs dans le modèle. C'est-à-dire, on a
\[
E\{Y\}=\beta_0+\beta_1\,x_1+\cdots+\beta_{p-1}\,x_{p-1}+\gamma_1\,\hat{y}^2+\gamma_2\,\hat{y}^3.
\]
Cela signifie que nous avons maintenant des effets d'ordre supérieur dans le modèle, que nous obtenons en ajoutant simplement deux paramètres dans le modèle, c.-à-d. et \(\gamma_1\) et \(\gamma_2\). Le test RESET de Ramsey est de tester
\[
H_0: \gamma_1 = \gamma_2 = 0 ~~~ \mbox{ contre } ~~~ Ha: \gamma_1 \neq 0 \mbox{ ou } \gamma_2 \neq 0.
\]
Si le test RESET de Ramsey est significatif, alors nous avons des preuves d’effets d’ordre supérieur manquants dans le modèle. Cela signifie que nous avons des preuves significatives qu'il y a une erreur dans la spécification de la fonction de la moyenne.
Remarque: le test de Ramsey est général dans le sens où il peut identifier des erreurs dans la spécification du modèle. Cependant, il ne peut pas nous dire quelle est la cause de l'erreur. Cela signifie qu'il y a des effets non linéaires. Nous devons étudier la relation partielle entre Y et les prédicteurs et essayer de trouver une relation non linéaire. Alternativement, la non-linéarité pourrait être causée par des interactions entre les prédicteurs.
Exemple [SAT 1999]: Considérons les données de une étude des résultats aux examens SAT aux Etats-Unis en 1999.
Les données sont dans le fichier :
sat.csv.
> SAT<-read.csv("sat.csv")
> mod<-lm(totalSAT99~Avg.teacher.salary+Percent.taking,data=SAT)
> # diagramme des résidus
> plot(mod,which=1)
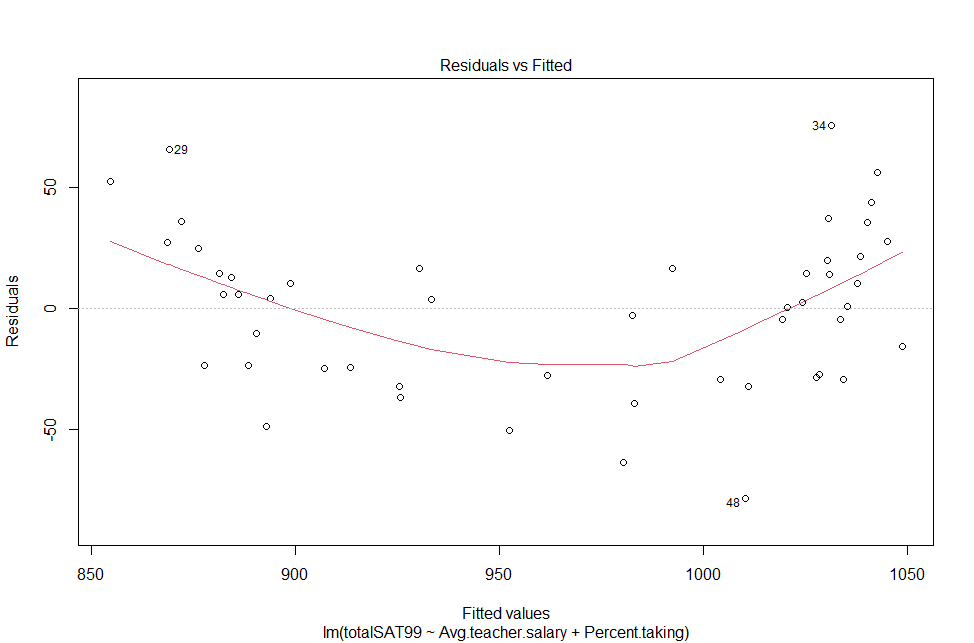
Le graphique des résidus suggère que la fonction de la moyenne n'est pas bien spécifiée. Nous effectuerons le test RESET de Ramsey à partir de la librarie lmtest. Il y a des preuves significatives d'une erreur dans la spécification du modèle
(\(F(1,45)=13,\!695; p<,\!0001\)).
> library(lmtest)
> library(lmtest)
> resettest(mod,power=c(2,3))
RESET test
data: mod
RESET = 13.695, df1 = 2, df2 = 45, p-value = 2.262e-05
Remarque: On peut performer le test RESET sans la librairie lmtest.
> # ajuste notre modèle
> mod<-lm(totalSAT99~Avg.teacher.salary+Percent.taking,data=SAT)
> # calculons le carré et le cube des valeurs ajustées
> y.ca<-mod$fitted.values^2
> y.cu<-mod$fitted.values^3
> # ajoutons le carré et le cube des valeurs ajustées au modèle
> modRESET<-lm(totalSAT99~Avg.teacher.salary+Percent.taking
+ +y.ca+y.cu,data=SAT)
> # comparer les deux modèles
> anova(mod,modRESET)
Analysis of Variance Table
Model 1: totalSAT99 ~ Avg.teacher.salary + Percent.taking
Model 2: totalSAT99 ~ Avg.teacher.salary + Percent.taking + y.ca + y.cu
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 53338
2 45 33157 2 20181 13.695 2.262e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Diagramme de la composante plus résidu (Component plus residual plot en anglais):
Supposons que nous souhaitons visualiser la relation partielle entre \(y\) et \(x_2\) (c'est-à-dire en contrôlant pour \(x_1\) - c'est-à-dire en soustrayant l'effet de X1). Nous voulons tracer \(y- (b_0 + b_1\,x_1)\) contre \(x_2\) ou ceci est équivalent à \(e+b_2\,x_2\) contre \(x_2\). Ceci est dit un
Soit \(x_2\)=le taux de participation. Nous construisons son diagramme de la composante plus résidu. Le diagramme suggère que le lien partiel est non-linéaire. On peut essayer d'inclure \(x_2^2\) ou même \(x_2^3\) dans le modèle.
> # fit the model
> model<-lm(totalSAT99~Avg.teacher.salary+Percent.taking,data=SAT)
> # partial residual
> beta<-model$coefficients
> #e<-with(SAT,totalSAT99-(beta[1]+beta[2]*Avg.teacher.salary))
> e<-model$residuals
> with(SAT,scatter.smooth(Percent.taking,e+beta[3]*Percent.taking))
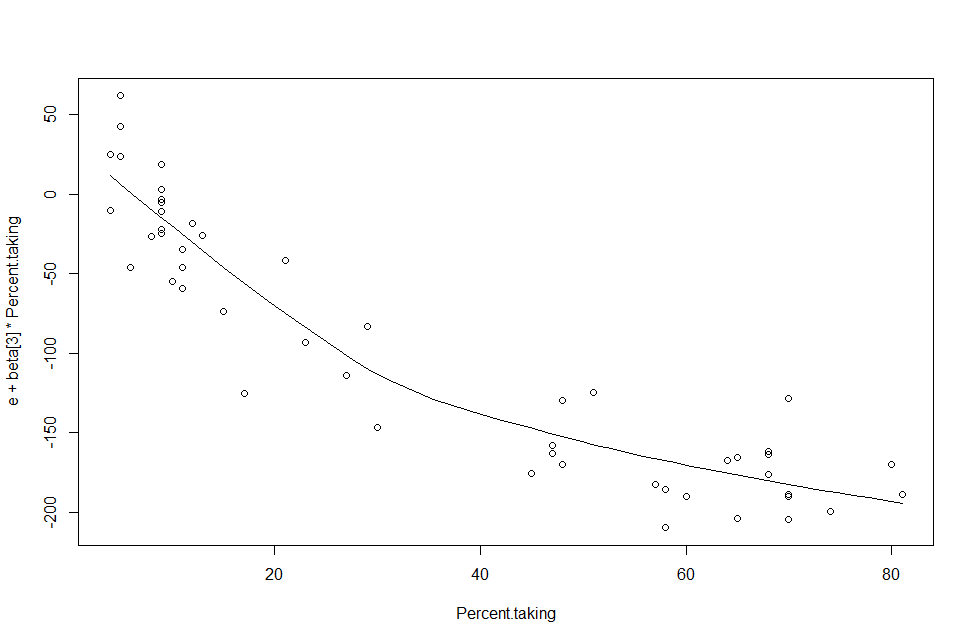
On peut utiliser la fonction crPlots de la librairie car pour construire les diagrammes.
> library(car)
Loading required package: carData
> crPlots(model,terms="Percent.taking")
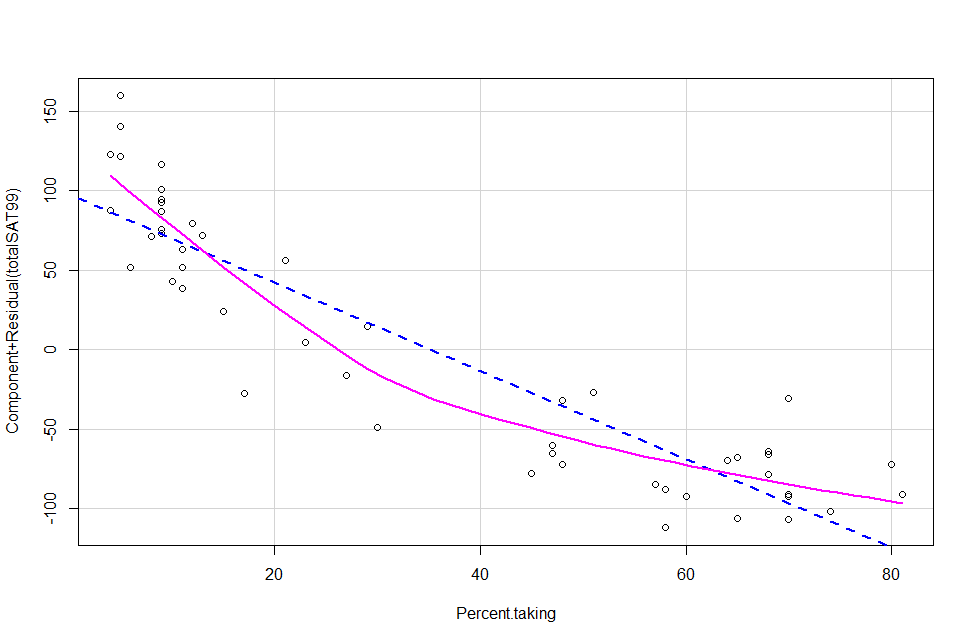
Voici les deux diagrammes.
> library(car)
> crPlots(model)
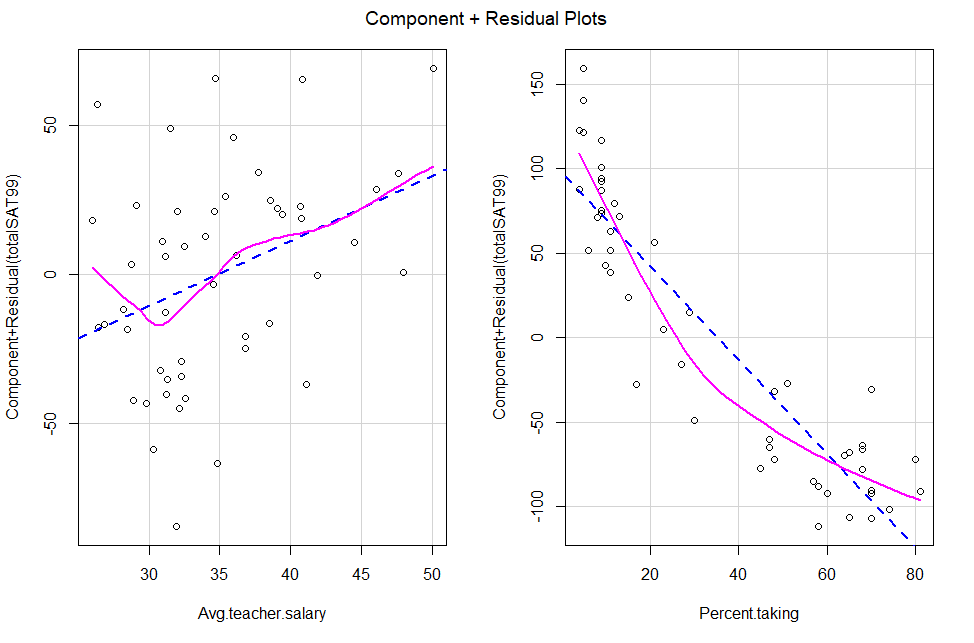
Exemple 36 : Diagnostique pour l'homoscédascité
Tension artérielle: Considérez que les données dans le fichier BloodPressure.csv.
Ce sont les données d'une étude de santé. Ils étudiaient l'association entre la pression artérielle diastolique et l'âge. Les participants étaient n = 54 femmes âgées de 20 à 60 ans. Nous importons les données et affichons quelques rangés.
> BP<-read.csv("BloodPressure.csv")
> head(BP)
Age DiastolicBP
1 27 73
2 21 66
3 22 63
4 24 75
5 25 71
6 23 70
Nous ajustons un modèle linéaire pour exprimer la pression artérielle diastolique en fonction de l'âge, et superposons la droite des moindres carrés sur le nuage de points de la pression artérielle en fonction de l'âge.
mod<-lm(DiastolicBP~Age,data=BP)
with(BP,plot(Age,DiastolicBP,ylab="Tension artérielle",xlab="Age"))
abline(mod)
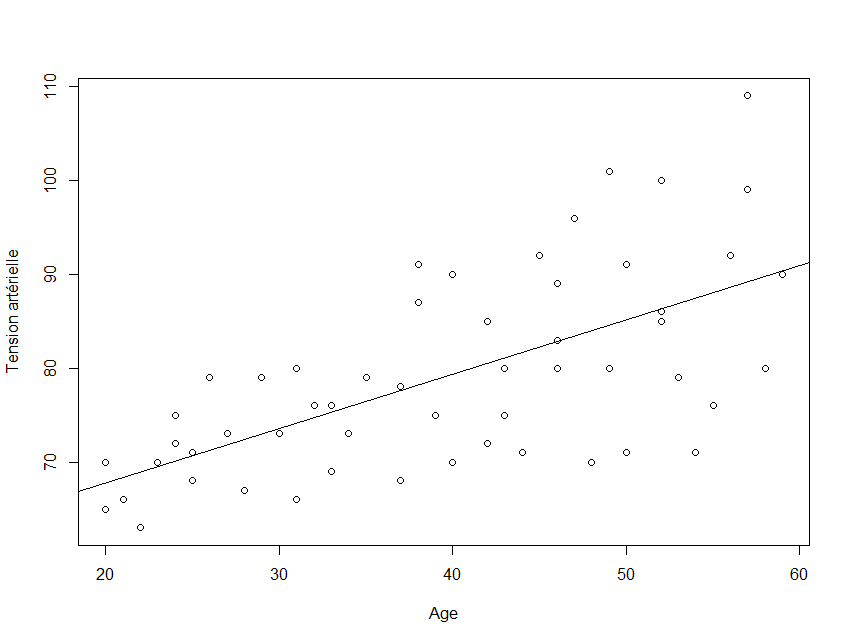 Le diagramme suggère que le lien est linéaire, mais que la variance n'est pas constante. La tension artérielle est plus variable pour les femmes plus âgées.
Le diagramme suggère que le lien est linéaire, mais que la variance n'est pas constante. La tension artérielle est plus variable pour les femmes plus âgées.
Remarques:
- Dans la pratique, on n'a pas toujours qu'un seul prédicteur. Alors, nous ne pouvons pas construire un nuage de points. Mais, on peut construire un diagramme d'échelle et localisation des résidus. C'est un nuage de points de \(\sqrt{|r_i|}\) contre (\hat{y}_i), où \(r_i=e_i/s\{e_i\}\) est un résidu studentisé. La tendance devrait être approximativement nulle proche de 1. Mais, si on observe une tendance dans le diagramme, alors ceci suggère que la variance de l'erreur n'est pas constante.
- On devrait premièrement vérifier que la fonction de la moyenne est bien spécifiée. Puisqu'une tendance dans le diagramme d'échelle et localisation des résidus peut être dû à un modèle mal-spécifié.
- On utilise l'argument
which=3 dans la fonction plot pour obtenir le diagramme d'échelle et localisation. Il y a une tendance dans le diagramme d'échelle et localisation des résidus. Ceci suggère que la variance de l'erreur n'est pas constante.
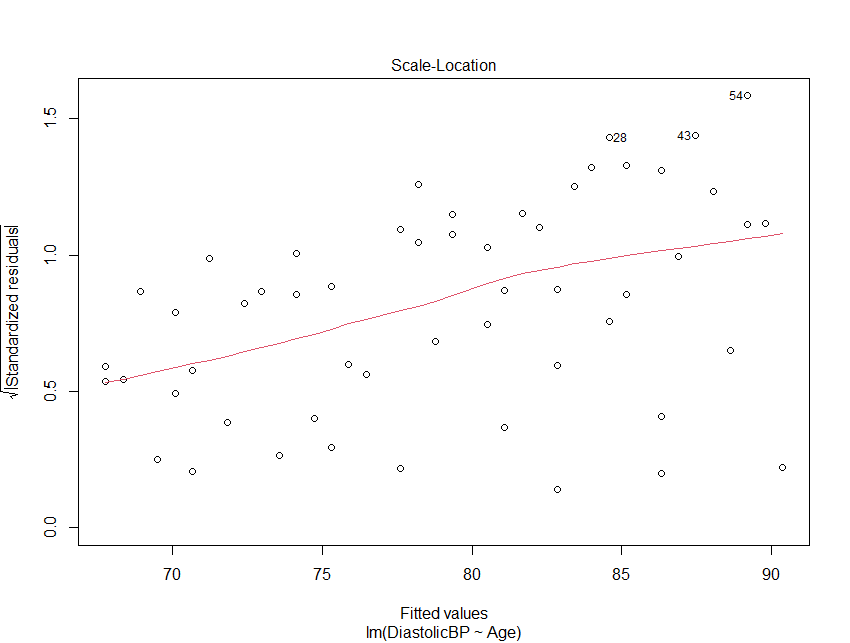
plot(mod,which=3)
Test d'hétéroscédasticité:
Nous discuterons de deux tests d'hétéroscédasticité: le test de Breusch-Pagan Studentizé et le test de White.
Considérons un modèle linéaire avec la fonction de la moyenne suivante :
\[
E\{Y\} = \beta_0 + \beta_1\,x_1 + \beta_2\,x_2 + \cdots + \beta_{p-1}\,x_{p-1}.
\]
Une condition sous-jacente du modèle linéaire est que la variance de l'erreur aléatoire est constante (homoscédasticité), c'est-à-dire \(V[\epsilon_i] = \sigma^2\), pour \(i = 1,\cdots, n\). En d'autres termes, la variance conditionnelle de Y étant donné \(X = x\) ne dépend pas de x. Cette hypothèse est parfois appelée une hypothèse d'homoscédasticité.
Le test de Breusch-Pagan Studentizé est réalisé comme suit:
- Étape 1: Ajustez le modèle linéaire avec la fonction de la moyenne ci-haut et obtenez les résidus \(e_1,\cdots, e_n\).
- Étape 2: Ajuster un modèle linéaire qui exprime le carré du résidu \(e^2\) selon \(x_1, x_2,\cdots, x_{p-1}\), et obtenir le coefficient de détermination correspondant \(R^2_{e^2 | x_1,\ldots,x_{p-1}}\).
- Étape 3: La statistique du test est \(R^2_{e^2 | x_1,\ldots,x_{p-1}}\).
- Étape 4: La valeur \(p\) est \(P(\chi^2(p - 1) \geq X^2_{BP})\).
Commentaires:
- Le test de Breusch-Pagan est appelé un test de score ou parfois un test de multiplicateur de Lagrange (test LM).
- Le test tente d'identifier l'hétéroscédasticité linéaire en \(x_1,\cdots, x_p\). Cependant, il est possible que l'hétéroscédasticité soit non linéaire en \(x_1,\cdots, x_n\). White (en 1980) a suggéré d'ajuster (e^2) selon les prédicteurs \(x_1, x_2,\cdots, x_{p-1}\), mais aussi d'ajouter des termes quadratiques et bilinéaires de \(x_1, x_2,\cdots, x_{p - 1}\) dans le modèle. Le nombre de paramètres à estimer pouvant être important, il est souvent difficile de réaliser ce test. Cependant, une simplification du test de White a été suggérée. Voir ci-dessous.
Test de White pour l'hétéroscédasticité à 2 degrés de liberté est effectué comme suit:
- Étape 1: Ajustez le modèle linéaire avec la fonction de la moyenne ci-haut et obtenez les résidus \(e_1,\cdots,e_n\) et les valeurs ajustées \(\hat{y}_1,\cdots,\hat{y}_n\).
- Étape 2: Ajustez le carré du résidu \(e^2\) par rapport à \(\hat{y\}\) et \(\hat{y}^2\), et obtenez le coefficient de détermination correspondant \(R^2_{e^2 | \hat{y}, \hat{y}^2}\).
- Étape 3: La statistique de test est \(X^2_{White} = n\,R^2_{e^2 | \hat{y}, \hat{y}^2}\).
-
Étape 4: La valeur \(p\) est \(P(\chi^2(2) \geq X^2_{White}).\)
D'après le test de Breusch-Pagan studentisé, il y a des preuves signficatives que la variance de l'erreur n'est pas contante \(X^2(1)=12,\!541; p=0,\!0004\).
> bptest(DiastolicBP~Age,data=BP)
studentized Breusch-Pagan test
data: DiastolicBP ~ Age
BP = 12.541, df = 1, p-value = 0.0003981
Commentaires:
- Le test de Breusch-Pagan suppose à titre d'alternative que la variance d'erreur est une fonction monotone des prédicteurs. Cependant, la fonction de la variance peut être plus complexe. Il pourrait y avoir des effets non linéaires que le test de Breusch-Pagan ne parvient pas à identifier.
- Un test alternatif est le test de White pour l'hétéroscédasticité à 2 degrés de liberté, qui peut être utile pour identifier une fonction de variance qui est une fonction non linéaire des prédicteurs.
- Le test de Breusch-Pagan et le test de White peuvent parfois contredire l'autre test. Voici quelques raisons:
- Si la variance d'erreur est une fonction monotone des prédicteurs, alors le test de Breusch-Pagan sera plus puissant que le test de White car le test de White est plus général. Donc, si le test de Breush-Pagan est significatif mais pas le test de White, il est possible que la taille d'échantillon n'est pas assez grande pour le test de White.
- Si la fonction de la variance est une fonction non linéaire complexe des prédicteurs, alors c'est le test de White qui sera plus puissant dans cette circonstance. Donc, si le test de White est significatif, mais que le test de Breusch-Pagan n'est pas significatif, alors il est très probable que la fonction de la variance soit une fonction non linéaire et complexe.
- Si la fonction de la moyenne n'est pas bien spécifiée, alors nous devons procéder avec prudence dans l'interprétation de la signification des tests d'hétéroskédascité. Ils pourraient simplement détecter l'erreur dans la spécification de la fonction de la moyenne.
D'après le test de White à 2 degrés de liberté, il y a aussi des preuves signficatives que la variance de l'erreur n'est pas contante \(X^2(1)=12,\!7; p=0,\!00179\).
> library(skedastic)
> model<-lm(DiastolicBP~Age,data=BP)
> white_lm(model)
# A tibble: 1 x 5
statistic p.value parameter method alternative
1 12.7 0.00179 2 White's Test greater
Exemple 37 : Correction de White pour l'hétéroscédasticité
Abordons les tests d'hypothèses concernant \(\beta = (\beta_0, \beta_1, \ldots, \beta_{p-1})'\) dans une perspective d'estimation. Nous savons que \( b = (b_0, b_1, \ldots, b_{p-1}) '\sim N (\beta, \mbox{Cov}\{b \}) \).
On peut démontrer que
\[
(b-\beta)'(\sigma^2\{b\})^{-1}(b-\beta) \sim \chi^2(p), ~~ \mbox{si \((\sigma^2\{b\})\) est inversible}.
\]
Mais, dans la pratique $\mbox{Cov}\{b\}$ est inconnue. Alors, on substitue \(\mbox{Cov}\{b\}\) avec \(\widehat{\mbox{Cov}}\{b\}\) qui est la matrice estimée des variances-covariances de \(b\).
Sous l'homoscédasticité, on a \(\mbox{Cov}\{b\}=\sigma^2\,(X'X)^{-1}\), et \(\widehat{\mbox{Cov}}\{b\}=\mbox{MSE}\,(X'X)^{-1}\). En supposant que \(\max_i h_{ii}\rightarrow 0\), quand \(n\rightarrow \infty\), on peut démontrer que
$$
(b-\beta)'(\widehat{\mbox{Cov}}\{b\})^{-1}(b-\beta)=\frac{(b-\beta)'(X'X)(b-\beta)}{MSE} \rightarrow \chi^2(p), ~~ \mbox{ quand \(n\rightarrow \infty\)},
$$
où la convergence est en distribution.
Sous l'hétéroscédasticité, la forme de la matrice des variances-covariances est un peu différente. On a
\[\sigma^2\{b\}=(X'X)^{-1}X' \mbox{Cov}\{\epsilon\} X(X'X)^{-1}, ~~~
\mbox{Cov}\{\epsilon\}=\begin{bmatrix}
\sigma_{1}^2 & 0 & 0 & \cdots & 0 \\
0 & \sigma_{2}^2 & 0 & \cdots & 0 \\
\vdots & & \ddots & & \vdots \\
0 & 0 & \cdots & 0 & \sigma_{n}^2 \\
\end{bmatrix}=\mbox{diag}(\sigma_1^2,\ldots,\sigma^2_n).
\]
Eicker en 1967 a démontrer que si on estime \(\mbox{Cov}\{\epsilon\}\) avec $\widehat{\mbox{Cov}}\{\epsilon\}=\mbox{diag}(e_1^2,\ldots,e_n^2)$, alors
$$
b'(\widehat{\mbox{Cov}}\{b\})^{-1}b=\frac{b's^2\{b\}b}{MSE} \rightarrow \chi^2(p), ~~ \mbox{ quand $n\rightarrow \infty$},
$$
où la convergence est en distribution, où \(\widehat{\mbox{Cov}}\{b\}=(X'X)^{-1}X' \mbox{diag}(e_1^2,\ldots,e_n^2) X(X'X)^{-1}\). Ce dernier estimateur de la matrice des variances-covariances est parfois nommé HC0 (pour heteroskedasticity constistent estimator et le 0 est puisqu'il fut le premier estimateur proposé). On l'appelle aussi parfois un estimateur sandwich . De nombreuses autres corrections d'hétéroscédasticité ont été proposées, et ont été appelées HC1, HC2, HC3, etc.
MacKinnon et White en 1985 ont fait une étude de simulation pour comparer les différents estimateurs HC. Ils suggèrent d'utiliser HC3, qui consiste à utiliser
\[
\widehat{\mbox{Cov}}\{\epsilon\}=\mbox{diag}(e_1^2/(1-h_{11})^2,\ldots,e_n^2/(1-h_{nn})^2).
\]
Calcul de la matrice de variance-covariance de $ b $ avec R: En supposant que mod est un modèle linéaire ajusté (c'est-à-dire un objet lm), alors vcov(mod) donne la matrice des variances-covariances pour $ b $. Cependant, nous devrons utiliser une librairie pour calculer HC3. Par exemple, on peut utiliser la fonction vcovHC de la librairie sandwich ou la fonction hccm de la librairie car .
Voici l'utilisation:
> ## supposons que mod est un objet lm
> ## matrice de variances-covariances sous l'homoscédascité
> vcov(mod)
> ## HC3 de sandwich
> library(sandwich)
> vcovHC(mod,type="HC3")
> ## HC3 de car
> library(car)
> hccm(mod,type="hc3")
Tension artérielle: Considérons les données de l'Exemple 36.
> BP<-read.csv("BloodPressure.csv")
> head(BP)
Age DiastolicBP
1 27 73
2 21 66
3 22 63
4 24 75
5 25 71
6 23 70
À l'Exemple 36, nous avons observé que ce n'est pas raisonnable de supposer que la variance de l'erreur est constante quand nous ajustons un modèle linéaire pour décrire la tension artérielle selon l'âge.
Voici la matrice des variances-covariances sous l'homoscédasticité.
> mod<-lm(DiastolicBP~Age,data=BP)
> vcov(mod)
(Intercept) Age
(Intercept) 15.9494301 -0.371977563
Age -0.3719776 0.009399527
Nous affichons maintenant nous affichons une matrice des variances-covariances consistente sous l'hétéroscédasticité.
> library(sandwich)
> vcovHC(mod,type="HC3")
(Intercept) Age
(Intercept) 11.4283657 -0.32783795
Age -0.3278379 0.01008658
> library(car)
> hccm(mod,type="hc3")
(Intercept) Age
(Intercept) 11.4283657 -0.32783795
Age -0.3278379 0.01008658
Le test linéaire général avec un modèle hétéroscédastique avec R:
- On peut comparer deux modèles linéaires avec la fonction
waldtest de la librairie lmtest.
> mod<-lm(DiastolicBP~Age,data=BP)
> library(sandwich)
> library(lmtest)
> mod0<-lm(DiastolicBP~1,data=BP)
> mod<-lm(DiastolicBP~Age,data=BP)
> waldtest(mod0,mod,vcov=vcovHC(mod,type="HC3"))
Wald test
Model 1: DiastolicBP ~ 1
Model 2: DiastolicBP ~ Age
Res.Df Df F Pr(>F)
1 53
2 52 1 33.355 4.348e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- On peut aussi faire des inférences concernant les paramètres du modèle avec une matrice HC3. Ceci est parfois dit des inférences avec des erreurs types robustes.
> coeftest(mod, vcov. = vcovHC(mod,type="HC3"))
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 56.15693 3.38059 16.6116 < 2.2e-16 ***
Age 0.58003 0.10043 5.7754 4.348e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> coefci(mod, level = 0.95, vcov. = vcovHC(mod,type="HC3"))
2.5 % 97.5 %
(Intercept) 49.3732861 62.9405726
Age 0.3784993 0.7815623
- Example (savings): We will be using a dataframe from the package
wooldridge. We start by loading the dataframe, and display a few rows.
> library(wooldridge)
> # Load the dataframe
> data("saving")
> head(saving)
sav inc size educ age black cons
1 30 1920 4 2 40 1 1890
2 874 12403 4 9 33 0 11529
3 370 6396 2 17 31 0 6026
4 1200 7005 3 9 50 0 5805
5 275 6990 4 12 28 0 6715
6 1400 6500 4 13 33 0 5100
Comment: The dataframe has 7 variables:
A data.frame with 100 observations on 7 variables:
- sav: annual savings;
- inc: annual income;
- size: family size;
- educ: years educ, household head
- age: age of household head
- black: =1 if household head is black
- cons: annual consumption
We start by fitting a linear model to describe the annual saving of the family as an additive function of income, size, education, and age. Then, using a general linear test with an HC variance-covariance matrix, we will test for the significance of each explanatory variable.
> mod<-lm(sav ~ inc + size + educ + age, data = saving)
> library(car)
> Anova(mod,type="III",white.adjust="hc3")
Coefficient covariances computed by hccm()
Analysis of Deviance Table (Type III tests)
Response: sav
Df F Pr(>F)
(Intercept) 1 0.2152 0.6438
inc 1 1.1517 0.2859
size 1 0.0868 0.7689
educ 1 0.6483 0.4227
age 1 0.0003 0.9863
Residuals 95
By default, the function Anova assumes homogeneity of variance. So if we take out the argument white.adjust, the result will be the same as using the drop1 function.
> Anova(mod,type="III")
Anova Table (Type III tests)
Response: sav
Sum Sq Df F value Pr(>F)
(Intercept) 2641392 1 0.2557 0.6143
inc 24116197 1 2.3343 0.1299
size 891684 1 0.0863 0.7696
educ 16052663 1 1.5538 0.2156
age 2682 1 0.0003 0.9872
Residuals 981478505 95
> drop1(mod,test="F")
Single term deletions
Model:
sav ~ inc + size + educ + age
Df Sum of Sq RSS AIC F value Pr(>F)
981478505 1619.9
inc 1 24116197 1005594701 1620.4 2.3343 0.1299
size 1 891684 982370188 1618.0 0.0863 0.7696
educ 1 16052663 997531168 1619.6 1.5538 0.2156
age 1 2682 981481187 1617.9 0.0003 0.9872
Exemple 38 : Diagnostique pour la normalité
Exemple: Nous importons les données du fichier commercial.csv et nous affichons quelques rangés. L'unité statistique est un immeuble commercial.
Les variables sont
- l'âge de l'immeuble;
- les frais d'exploitations;
- les taux d'inoccupation;
- la superficie en pieds carrés;
- les tarifs de locations (ceci est la variable dépendante).
> commercial<-read.csv("commercial.csv")
> head(commercial)
Age Operating.Expenses Vacancy.Rates Square.Footage Rental.Rates
1 13.5 1 5.02 0.14 123000
2 12.0 14 8.19 0.27 104079
3 10.5 16 3.00 0.00 39998
4 15.0 4 10.70 0.05 57112
5 14.0 11 8.97 0.07 60000
6 10.5 15 9.45 0.24 101385
Nous voulons décrire les tarifs de locations selon les autres variables.
Voici le modèle estimée
$$
\hat{y}=-521828,\!001+38000,\!343\,(\mbox{age}) +7427,\!809 \,(\mbox{frais.explotation}) +3754,\!888\,(\mbox{innocupation}) +152944,\!634\, \,(\mbox{superficie}).
$$
> mod<-lm(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,data=commercial)
Remarques: D'après notre modèle un erreur aléatoire \(\epsilon\) suit une loi \(N(0,\sigma^2)\). La moyenne de zéro fait seulement du sense si la fonction de la moyenne est bien spécifiée. En outre, si la variance n'est pas constante, alors les erreurs suivent des lois normales différentes. Ceci veut dire que nous pourrons pas tester pour la normalité dans ce cas. Alors, c'est important de vérifier la spécification de la fonction de la moyenne et de vérifier que la variance est constante, avant d'étudier la normalité des erreurs.
Le test de Shapiro-Wilk sur les résidus studentisées: On peut mettre les résidusés studentisés dans la fonction shapriro.test. Nous avons des preuves contre la normalité des erreurs \(W=0,\!9589; p=0,\!0176 \).
> shapiro.test(rstudent(mod))
Shapiro-Wilk normality test
data: rstudent(mod)
W = 0.95886, p-value = 0.01076
Commentaires:
-
Nous avons des preuves significatives contre la preuve de la normalité des erreurs. Mais, le nombre d'unités $n=81$ est grand. (Les test pour la normalité sont très puissant pour grand $n$ et ont peu de puissance pour des petites tailles d'échantillon, disons \(n < 40 \).
- Nous allons utilisé des outils visuels pour décrire la déviation de la normalité. Voici un diagramme quantile-quantile des résidus studentisés avec des intervalles de confiance ponctuelles. On observe des déviations à l'extrémité positive.
- Nous avons aussi produit un histogramme (de densité) des
résidus studentisés avec une superposition de la densité d'une loi $T(n-p-1)$. (On suggère d'utiliser un histogramme seulement si taille d'échantillon est assez grande.) On observe que la déviation n'est pas grande. La distribution des résidus studentisés a une faible asymétrie positive. Puisque la déviation contre la normalité est faible et que la taille de l'échantillon est grande, alors c'est raisonnable de supposer que l'erreur est approximativement normalement distribuée.
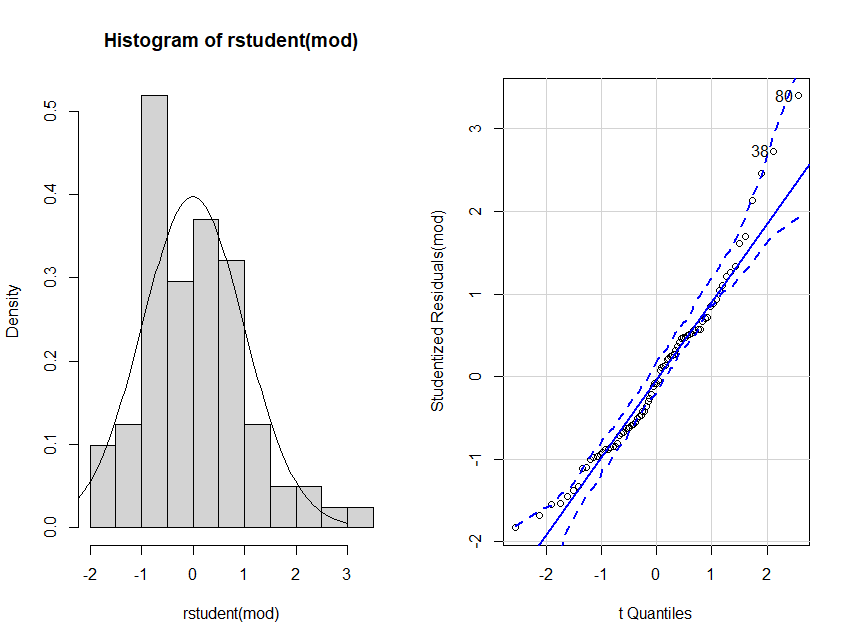
> par(mfrow=c(1,2))
> hist(rstudent(mod),prob=TRUE)
> curve(dt(x,mod$df.residual-1),-3,3,add=TRUE)
> library(car)
> qqPlot(mod)
[1] 38 80
Exemple 39 : Construire un modèle
Quelques stratégies: De Kutnel et al. :
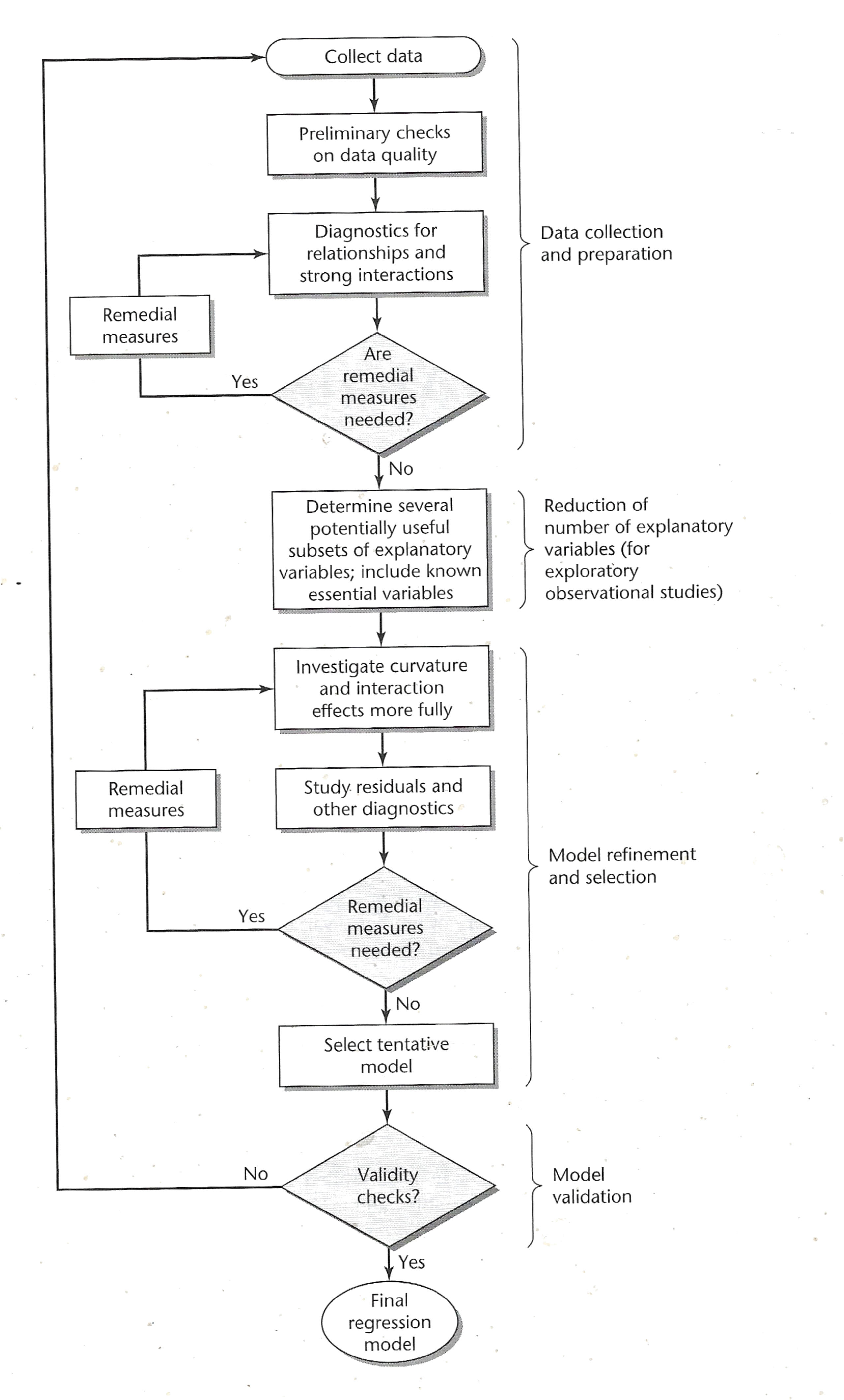 Alternative: Référence: Applied Logistic Regression, 3rd Edition, David W. Hosmer Jr., Stanley Lemeshow, Rodney X.
(1) Construire un modèle initial d'effets principaux en utilisant des variables explicatives qui incluent les variables connues importantes et d'autres qui montrent toute évidence d'être pertinente lorsqu'elles sont utilisées comme un seul prédicteur ( par exemple, valeur-\(p < 0,\!2\) ).
Alternative: Référence: Applied Logistic Regression, 3rd Edition, David W. Hosmer Jr., Stanley Lemeshow, Rodney X.
(1) Construire un modèle initial d'effets principaux en utilisant des variables explicatives qui incluent les variables connues importantes et d'autres qui montrent toute évidence d'être pertinente lorsqu'elles sont utilisées comme un seul prédicteur ( par exemple, valeur-\(p < 0,\!2\) ).
(2) Effectuer une élimination descendante en conservant une variable si elle est soit significative à un niveau plus strict, soit montre qu'elle est un facteur de confusion pertinent, en ce sens que l'effet estimé d'une variable clé change considérablement lorsqu'elle est supprimée.
(3) Ajouter au modèle toutes les variables qui n'étaient pas incluses à l'étape 1 mais qui sont significatives lors de l'ajustement de la variable dans le modèle après l'étape 2, puisqu'une variable n'est pas associée de manière significative à y mais peut apporter une contribution importante à la présence d'autres variables.
(4) Vérifier les interactions plausibles entre les variables du modèle après l'étape 3, en utilisant un niveau de signification de 5%.
(5) Effectuer des diagnostiques.
Sélection d'un sous-ensemble de prédicteurs
- Meilleur sous-ensemble:
Supposons que nous ayons une étude exploratoire et que nous souhaitons déterminer le meilleur sous-ensemble de prédicteurs pour décrire la distribution de la variable dépendante.
Considérez les données de Hitters.csv. Nous convertissons les vecteurs de caractères en facteurs. Il s'agit des données de la Ligue majeure de baseball des saisons 1986 et 1987. Il a 322 observations de joueurs de ligues majeures sur 20 variables.
> hitters<-read.csv("Hitters.csv",stringsAsFactors=TRUE)
> str(hitters)
'data.frame': 322 obs. of 20 variables:
$ AtBat : int 293 315 479 496 321 594 185 298 323 401 ...
$ Hits : int 66 81 130 141 87 169 37 73 81 92 ...
$ HmRun : int 1 7 18 20 10 4 1 0 6 17 ...
$ Runs : int 30 24 66 65 39 74 23 24 26 49 ...
$ RBI : int 29 38 72 78 42 51 8 24 32 66 ...
$ Walks : int 14 39 76 37 30 35 21 7 8 65 ...
$ Years : int 1 14 3 11 2 11 2 3 2 13 ...
$ CAtBat : int 293 3449 1624 5628 396 4408 214 509 341 5206 ...
$ CHits : int 66 835 457 1575 101 1133 42 108 86 1332 ...
$ CHmRun : int 1 69 63 225 12 19 1 0 6 253 ...
$ CRuns : int 30 321 224 828 48 501 30 41 32 784 ...
$ CRBI : int 29 414 266 838 46 336 9 37 34 890 ...
$ CWalks : int 14 375 263 354 33 194 24 12 8 866 ...
$ League : Factor w/ 2 levels "A","N": 1 2 1 2 2 1 2 1 2 1 ...
$ Division : Factor w/ 2 levels "E","W": 1 2 2 1 1 2 1 2 2 1 ...
$ PutOuts : int 446 632 880 200 805 282 76 121 143 0 ...
$ Assists : int 33 43 82 11 40 421 127 283 290 0 ...
$ Errors : int 20 10 14 3 4 25 7 9 19 0 ...
$ Salary : num NA 475 480 500 91.5 750 70 100 75 1100 ...
$ NewLeague: Factor w/ 2 levels "A","N": 1 2 1 2 2 1 1 1 2 1 ...
Il manque des valeurs dans la variable dépendante. Supprimons ces observations.
> # number of missing values
> sum(is.na(hitters$Salary))
[1] 59
> # remove observations with a missing response
> is.not.na<-!is.na(hitters$Salary)
> hitters<-hitters[is.not.na,]
Nous ajustons un modèle linéaire.
> mod <-lm(Salary~.,data=hitters)
Description de l'ajustement: Les trois statistiques suivantes sont équivalentes dans le sense qu'elles sont toutes des fonctions (monotones) de la somme de carrés résiduelle SSE :
- la somme de carrés résiduelle est
\[
\mbox{SSE}=\sum_{i=1}^n (y_i-\hat{y}_i)^2=24,200,700;
\]
- le coefficient de détermination est
\[
R^2=\frac{s_{yy}}-\mbox{SSE}}{s_{yy}}=1-\frac{\mbox{SSE}}{s_{yy}}=0.5461;
\]
- le max du log de vraisemblance:
\[
\ell=-\frac{n}{2}-\frac{n}{2}\,\ln\left(\frac{2\,\pi\,\mbox{SSE}}{n} \right)=-1876.191.
\]
Commentaires: Pour un jeu de données en particulier, \(n\) est fixe et \(s_{YY}\) est fixe quels que soient les prédicteurs que nous utilisons. Ainsi, les trois statistiques ci-haut sont simplement des fonctions de SSE.
> ## SSE
> sum((mod$residuals)^2)
[1] 24200700
> ## coefficient de détermination
> summary(mod)$r.squared
[1] 0.5461159
> ## max du log de vraisemblance
> ## df est le nombre de paramètres dans le modèle
> ## df=nombre de coefficients + 1 ( 1 pour sigma)
> logLik(mod)
'log Lik.' -1876.191 (df=21)
Dans une étude exploratoire, nous avons souvent un grand nombre de variables explicatives. Notre objectif est de trouver un modèle simple qui est le meilleur dans un certain sens pour décrire la distribution de la variable dépendante.
Notre problème comporte un petit nombre de variables explicatives pour faciliter l'illustration des méthodes. Un modèle qui comporte trop de variables explicatives souffre souvent d'un surapprentissage (également appelé sur-ajustement) qui se traduit souvent par une plus grande variance dans l'estimation des paramètres et réduit la valeur prédictive du modèle.
Critères pour identifier le meilleur sous-ensemble de prédicteurs: Nous comparerons les modèles. Soit \(P\) le nombre de coefficients dans le modèle complet . Ici \(P = 20 \).
Nous ne devons pas utiliser SSE, ni \(R^2\), ni le max du log de vraisemblance pour comparer les modèles car cela favorisera toujours le modèle complet avec tous les \(P-1\) prédicteurs du modèle.
Nous commencerons par ajuster le modèle complet avec tous les \( P-1 = 19 \) prédicteurs .
> mod <-lm(Salary~.,data=hitters,x=TRUE,y=TRUE)
> ## extract the matrix of the predictors (without the columns of 1's) [ x1 x2 ... x_{p-1}]
> x<-mod$x[,-1]
> ## extract the names of the variables
> var.names <- colnames(x)
> ## extract the response variable
> y<-mod$y
Commentaires: Notez que nous ajoutons les arguments x = TRUE et y = TRUE à la fonction lm .
Cela nous permettra d'extraire la matrice du plan et les valeurs de y que nous utiliserons dans la fonction leaps ci-dessous.
Nous présenterons quelques statistiques qui ont été développées pour la comparaison de modèles.
La puissance des tests d'hypothèse et la précision de nos estimations sont affectées par la variance de l'erreur et le nombre de degrés de liberté de l'erreur \(n-p\). Si nous réduisons le nombre de variables explicatives, nous aurons un gain en nombre de degrés de liberté qui pourrait conduire à des estimations plus précises si la variance de l'erreur n'est pas trop grande. Pour décrire ce gain en nombre de degrés de liberté, on pourrait comparer \(MSE = \mbox{SSE} / (n-p) \) à \(s_Y^2 = \sum_{i = 1}^n (Y_i- \bar{Y})^2 / (n-1) \) au lieu de comparer
SSE à \(s_{yy}\). On obtient le coefficient de détermination ajusté:
\[
R_a^2 = 1-\frac{MSE}{s_Y^2} = 1- \frac{(n-1)}{(n-p)} \frac{SSE}{s_{yy}}.
\]
Le coefficient de détermination ajusté est \(R_a^2=0.5106.\)
> summary(mod)$adj.r.squared
[1] 0.510627
On peut utiliser la fonction leaps de la librairie leaps pour calculer \(R^2_a\) pour tous les sous-modèles. Nous avons \(2^{P-1}-1=2^{4}-1=16-1=15\) modèles si on ne compte pas le modèles sans variables explicatives.
> library(leaps)
> search<-leaps(x=x, y=y,method="adjr2")
Voici des commandes pour construire un tableau.
num.models<-nrow(search$which)
all.models<-search$which
model.name<-character(num.models)
for(i in 1:num.models)
{
model.name[i] = paste(var.names[all.models[i,]], collapse=" ")
}
results<-data.frame(model.name,search$size,search$adjr2)
colnames(results)=c("model", "size","R2-a")
results contient \(R^2_a\) pour tous les modèles. Nous allons extraire le meilleur modèle selon $R^2_a$.
> results[which.max(search$adjr2),]
model size R2-a
101 AtBat Hits Walks CAtBat CRuns CRBI CWalks LeagueN DivisionW PutOuts Assists 12 0.5225706
- Une autre approche consiste à utiliser une approche par critère d'information. Voici le critère d'information d'Akaike (AIC):
\[
\mbox{AIC}=2\,(K-\ell), ~~~ \mbox{ où \(\ell\) est le max de vraisemblance}
\]
et \(K=p+1\) est le nombre de paramètres qu'on doit estimer. Il y a \(p\) coefficients pour estimer la moyenne et 1 paramètre pour \(\sigma\). Pour le modèle complet, on a \(\mbox{AIC}=3794,\!383\).
> AIC(mod)
[1] 3794.383
Interpretation: Suppose that there is a true probability distribution (that is unknown) that explains $Y$ as a function of $X$. We will impose a parametric family to describe this distribution with a linear model. There is an
measure of divergence called Kullback-Leibler that measures the loss of information that results from using this parametric family. The more this measure of divergence is small, the smaller the loss of information. Akaike showed
that we can estimate this measure of divergence with
$c+2\,(K-\ell)$, where $c$ is a constant that depends on the true distribution that is unkown. However, is is not necessary to know $c$ to compare models. The model with the smallest AIC will have the smallest loss of information.
Comment: A smaller AIC is better. To have a smaller AIC, we need SSE to be small, but we also need the number of coefficients to be too large. So AIC favours simpler models that fit well.
Here we use the function ```bestglm``` from the ```bestglm``` package to find the best subset according to AIC.
> Xy<-cbind(as.data.frame(x),y)
> library(bestglm)
> out<-bestglm(Xy)
> names(out)
[1] "BestModel" "BestModels" "Bestq" "qTable" "Subsets" "Title"
[7] "ModelReport"
> out$BestModel
Call:
lm(formula = y ~ ., data = data.frame(Xy[, c(bestset[-1], FALSE),
drop = FALSE], y = y))
Coefficients:
(Intercept) AtBat Hits Walks CRBI DivisionW PutOuts
91.5118 -1.8686 7.6044 3.6976 0.6430 -122.9515 0.2643
## Stepwise methods
When the number of parameters is large, the number of sub-models can be enormous, and we will not be able to fit all possible models. Another way to approach the problem is to use a stepwise selection method.
We will need a data frame that has only the response variable and the predictors.
Forward selection:
- We start with the model without any explanatory variables. This is called the null model.
- Then, we add a variable in the model according to AIC.
- We continue to add predictors into the model until we cannot improve AIC.
We fit the null model (only the intercept) with R, and the full model with all the predictors. We then give the null model to the function step, and we indicate that we want a forward direction, and we give the formula for the full model in the scope argument.
```{r }
mod <-lm(Salary~.,data=hitters)
mod0<-lm(Salary~1,data=hitters)
step(mod0,direction="forward",scope=formula(mod),trace=0)
```
Backward selection:
- We start with the full model.
- We then delete a predictor from the model according to AIC.
- We continue to remove predictors until we cannot improve AIC.
```{r }
step(mod,direction="backward",trace=0)
```
Stepwise selection:
- We start with either the null model or the full model.
- At each iteration, we have a forward step and a backward step.
- We continue until we cannot improve AIC.
```{r }
step(mod,direction="both",trace=0)
```
Exemple 40 : Aberrance en X et en Y -- Influence
Exemple: Nous importons les données du fichier commercial.csv et nous affichons quelques rangés. L'unité statistique est un immeuble commercial.
Les variables sont
- l'âge de l'immeuble;
- les frais d'exploitations;
- les taux d'inoccupation;
- la superficie en pieds carrés;
- les tarifs de locations (ceci est la variable dépendante).
> commercial<-read.csv("commercial.csv")
> head(commercial)
Age Operating.Expenses Vacancy.Rates Square.Footage Rental.Rates
1 13.5 1 5.02 0.14 123000
2 12.0 14 8.19 0.27 104079
3 10.5 16 3.00 0.00 39998
4 15.0 4 10.70 0.05 57112
5 14.0 11 8.97 0.07 60000
6 10.5 15 9.45 0.24 101385
Voici le modèle estimée
y^=−521828,001+38000,343(age)+7427,809(frais.explotation)+3754,888(innocupation)+152944,634(superficie).
> summary(mod)$coefficients
Estimate Std. Error t value Pr(>|t|)
(Intercept) -521828.001 86088.481 -6.0615310 4.834440e-08
Age 38000.343 6640.577 5.7224457 1.975990e-07
Operating.Expenses 7427.809 1652.664 4.4944461 2.456686e-05
Vacancy.Rates 3754.888 4895.931 0.7669406 4.454928e-01
Square.Footage 152944.634 73352.435 2.0850655 4.042145e-02
Remarques: L'estimation du modèle peut être influencer par des unités aberrantes. Alors, nous allons apprendre à identifier des unités qui pourrait être aberrant en X, en Y, ou même en X et Y.
Aberrance ~:~ Nous allons présenter les idée dans le cas d'une modèle simple.
- Nous allons dire qu'une unité est aberrante en X, si ces valeurs des variables indépendantes sont très différentes des autres. Pensons en terme de s'éloigner du centre.
Voici un nuage de point pour illustrer ce concept.
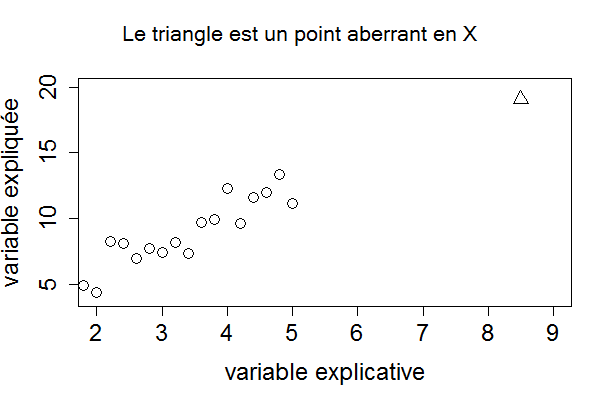
- Les points, en général, vont suivre une certaine tendance (qui peut être linéaire ou non-linéaire).
Nous allons dire qu'une unité est aberrante en Y, si sa distance de cette tendance est très différentes des autres. Pensons en terme de s'éloigner du centre, mais conditionnelle sur X.
Voici un nuage de point pour illustrer ce concept.
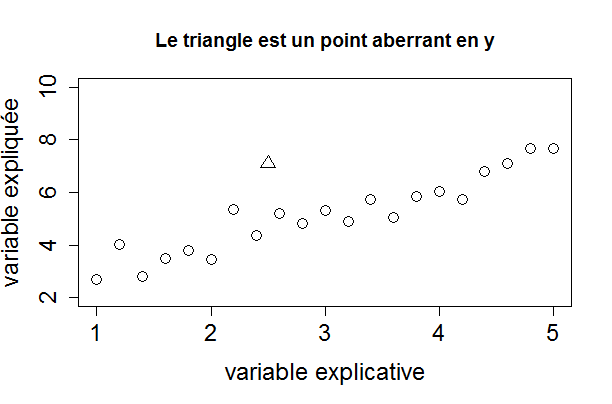
- Une unité peut être aberrant en X et aberrant en Y. Ces unités peuvent avoir une grande influence sur l'ajustment du modèle linéaire.
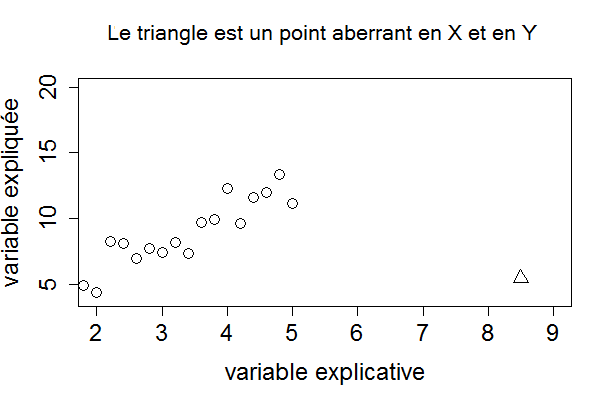
Identifier des unités aberrante en X --- La matrice chapeau et les valeurs leviers:
Considérons la matrice chapeau (dit hat matrix en anglais par John Tukey) :
H=X(XX)−1X′, où X est la matrice du plan.
Rappel: Y^=HY, alors la i-ème valeur ajustée est une combinaire des n valeurs observées~:~
y^i=hi1y1+hi2y2+…+hinyn.
On va utiliser la matrice chapeau pour identifier des unités aberrantes en X.
Définition: Soit Xn×p la matrice du plan pour un mod\`ele lin\'eaire. Soit x∗=(1,x1,x2,…,xp−1)′ un vecteur de Rp.
La valeur levier de ce point est
h∗=[1,x1,x2,…,xp](XX)−1⎡⎣⎢⎢⎢⎢1x1…xp⎤⎦⎥⎥⎥⎥.
En anglais, on dit leverage ou hat value.
Remarques:
- Chaque unité dans notre échantillon a un levier
xi(XX)−1x′i=hii ← la ième composante dans la diagonale de H,
où xi est la ième rangé de la matrice du plan.
- Le levier est 1/n plus une distance élliptique entre x∗=(x1,x2,…,xp)′ et le centroide x¯=(x¯1,x¯2,…,x¯p)′ (qui prend en considération
la variabilit\'e dans les X. Dans le cas simple, le levier pour x∗ est
h=1n+(x∗−x¯)2sxx.
- Pour visualiser le levier, considérons un modèle avec seulement deux variables explicatives. Considérons le jeu de données
commercial. Considérons un modèles avec p=2 variables explicatives : x1=age et le x2=taux d'inoccupation.
Nous ajustons le modèle avec la fonction de la moyenne
E{Y}=β0+β1(age)+β23754,888(innocupation),
et nous construisons un nuage de points de x1 contre x2 en superimposant la valeur du levier pour chaque unité.
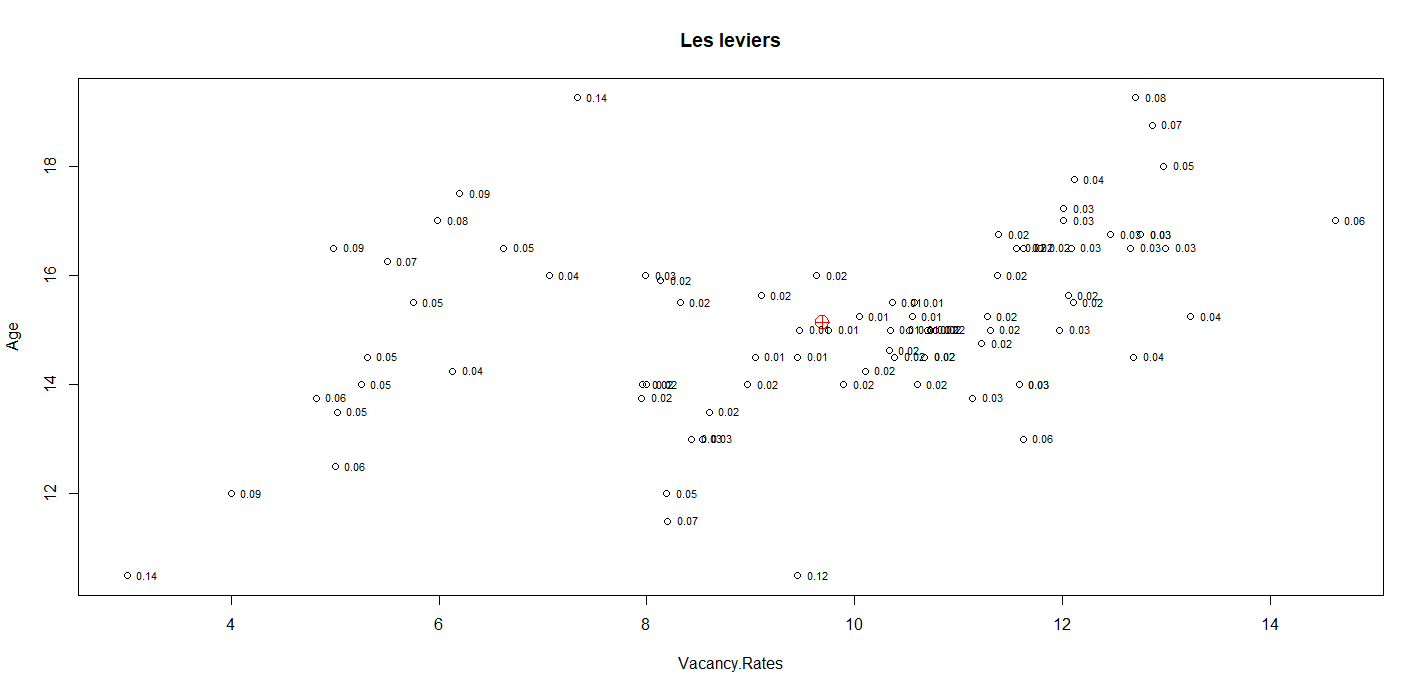
with(commercial,plot(Age~Vacancy.Rates,main="Les leviers"))
with(commercial,points(mean(Vacancy.Rates),mean(Age),cex=2,col="red",pch=10))
mod<-lm(Rental.Rates~Vacancy.Rates+Age,data=commercial)
## le vecteur des leviers
levier<-lm.influence(mod)$hat
with(commercial,text(Vacancy.Rates,Age,labels=round(levier,2), cex= 0.7,pos=4))
Dans la pratique, on pourrait avoir plus que 2 variables, alors on produit plutôt un diagramme des leviers selon l'indice de l'unité. Considérons notre exemple où nous voulons décrire
le tarif de location d'un immeuble commercial selon son age, les frais d'exploitations, le taux d'inoccupation, et la surperficie en pieds carrés.
Voici un diagramme des leviers. On affiche l'indice des unités qui ont les 5 plus grands leviers. Par exemple, l'unité 61 a le plus grand levier (h61,61=0,3099).
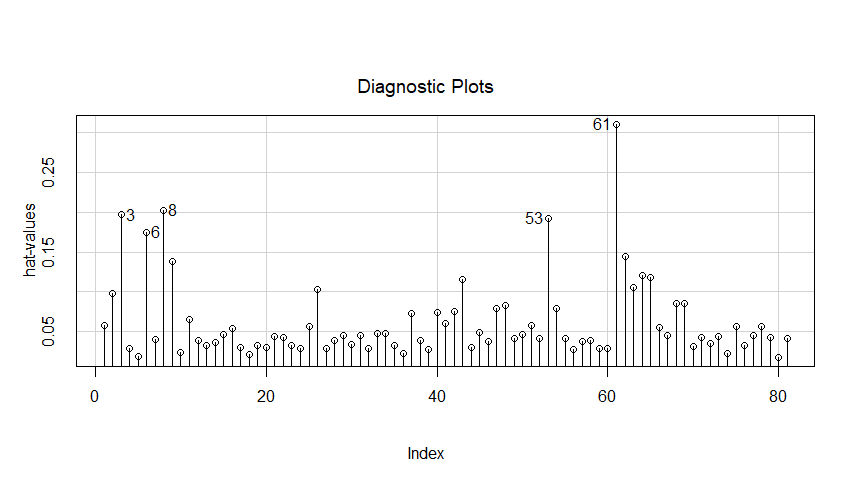
> mod<-lm(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,data=commercial)
> library(car)
> infIndexPlot(mod,vars="hat",id=list(method="y", n=5, cex=1, col=carPalette()[1], location="lr"))
> levier<-lm.influence(mod)$hat
> sort(levier,decreasing=TRUE)[1:5]
61 8 3 53 6
0.3099391 0.2019926 0.1966052 0.1918374 0.1747175
D'où vient le nom levier? (leverage en anglais)} On peut d\'emontrer que
hii(1−hii)=∑j=1 : i≠jnh2ij≥0.
Alors, 0≤hii≤1. En outre, quand hii s'approche de 1, on aura ∑j=1 : i≠jnh2ij≈0 et hij≈0 pour i≠j.
Mais,
y^i=hiiyi+∑j=1 : i≠jnhijyi et e^i=yi−y^i=(1−hii)yi+∑j=1 : i≠jnhijyi.
Alors, quand hii s'approche de 1, on aura y^i≈yi (alors sa valeur ajust\'ee va d\'ependre approximativement seulement de sa valeur observ\'ee) et
e^i≈0 (alors son r\'esidu sera presque nulle, quelque soit sa valeur observée). Le modèle estimée passera par le centroide et proche de ce point avec un tr\`es grand levier.
Démontration : Puisque H=H2, on a
hii==∑j=1nhijhji=∑j=1nhijhij ( puisque H est sym\'etrique)h2ii+∑j=1: i≠jnh2ij.
Alors,
hii(1−hii)=∑j=1: i≠jnh2ij.
Ceci est la fin de la démonstration.
La moyenne des leviers est
h¯=∑ni=1hiin=tr(H)n=tr(X(X′X)−1X′)n=tr(X′X(X′X)−1)n=tr(Ip)n=pn.
Identification des unités aberrantes en X : On dit que l'unité i
- est aberrant en X si hii>3p/n, où p/n= la moyenne des leviers;
- a un grand levier si hii>0,5;
- a un levier modéré si 0,2<hii≤0,5.
- est aberrant en X si hii est le plus grand levier l'écart avec le deuxième plus grand levier est grand.
Dans notre exemple des immeubles commerciaux, les unités 3, 8, 53 et 61 sont aberrants en X, mais seulement 8 et 61 ont un levier modéré. Aucune unité a un grand levier.
> mod<-lm(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,data=commercial)
> levier<-lm.influence(mod)$hat
> levier[levier>3*mean(levier)]
3 8 53 61
0.1966052 0.2019926 0.1918374 0.3099391
> levier[levier>0.5]
named numeric(0)
> levier[levier>0.2]
8 61
0.2019926 0.3099391
Aberrance en Y: Rappelons-nous que e∼N(0;σ2(I−H)). Si on estime σ2, avec la variance résiduelle MSE, alors peut calculer le résidu standardisé
pour chaque unité :
ri=eis(ei)=eiMSE−−−−√1−hii−−−−−−√, pour i=1,2,…,n.
On pourrait utiliser la règle suivante pour identifier des unités aberrantes en Y~:~
i est aberrante en Y, si |ri|>3.
Selon notre règle, l'unité 80 parmi les immeubles commerciaux est aberrante en Y.
> rstandard(mod)[abs(rstandard(mod))>3]
80
3.184845
Quel est le problème avec cette méthode? Si nous avons une unité avec un très grand levier, alors son résidu sera petit à cause de sa grande influence sur l'ajustment.
Solution au problème : Utilisons plutôt, l'erreur prévue pour l'unité i :
ei(i)=yi−y^i(i), pour i=1,2,…,n.
N.B.: y^i(i) est la valeur prévu pour l'unité i en ajustant le modèle sans l'unité i.
Avec un peu d'algèbre linéaire, on peut démontrer que
e^i(i)=ei1−hii, pour i=1,2,…,n.
Alors, ce n'est pas nécessaire de ré-ajuster le modèle n fois pour calculer les résidu prévu. Ensuite, on obtient le résidu studentisé (externe)
ti=ei(i)s(ei(i))=ei(n−p−1SSE(1−hii)−e2i)1/2, pour i=1,2,…,n.
L'unité i est dite aberrante en Y, si |ti|>3. C'est-à-dire, que son résidu studentisé (externe) est grand.
Pour les immeubles commerciaux, l'unit\'e 80 est aberrant en Y, puique |ti|=3,399≥3.
> rstudent(mod)[abs(rstudent(mod))>3]
80
3.398747
Voici un diagramme des résidus studentisés pour identifier les unit\'es aberrantes en Y.
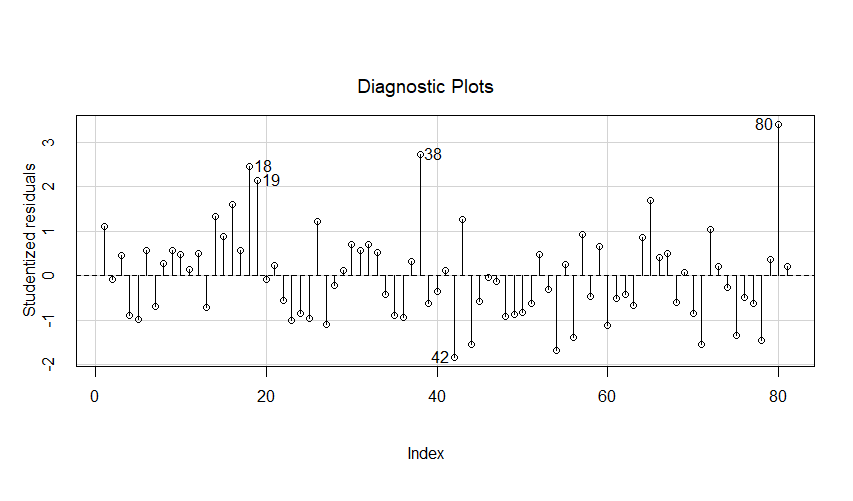
> libary(car)
> infIndexPlot(mod,vars="Studentized",id=list(method="y", n=5, cex=1, col=carPalette()[1], location="lr"))
Influence:
Encore plus important que l'aberrance de l'unité est la description de son influence sur l'ajustement. Nous allons introduire la distance de Cook pour décrire l'influence de l'unité i.
- La distance de Cook est utilisé pour décire l'influence de l'unité sur toutes les valeurs ajustées. Elle est
Di=∑nk=1(y^k−y^k(i))2pMSE=e2ipMSE(hii(1−hii)2).
- On dit que l'unité i a une grande influence sur les valeurs ajustées
si Di>F(0,5;p,n−p).
- On dit que l'unité i a aucune ou une petite influence sur les valeurs ajustées
\[
\mbox{ si } ~ D_i < F(0,\!2;p,n-p).
\]
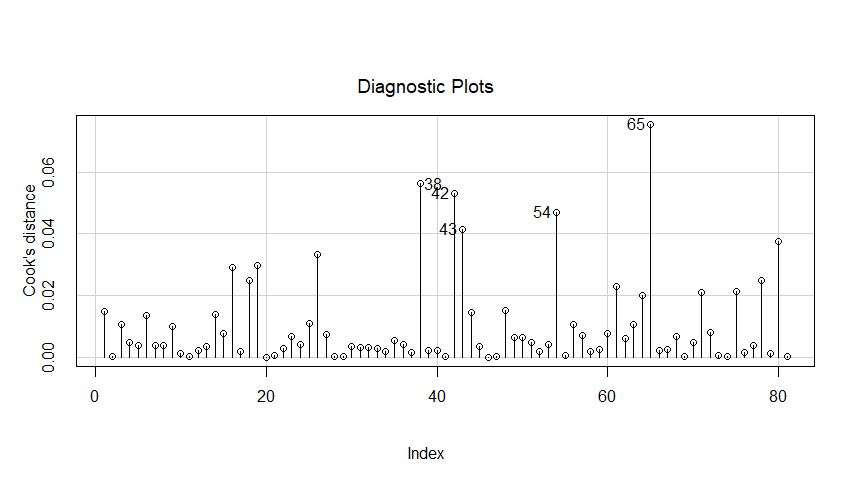
> mod<-lm(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,data=commercial)
> library(car)
> infIndexPlot(mod,vars="Cook",id=list(method="y", n=5, cex=1, col=carPalette()[1], location="lr"))
> p<-length(mod$coefficients)
> cooks.distance(mod)[cooks.distance(mod)>qf(0.5,p,mod$df.residual)]
named numeric(0)
Remarque: La distance de Cook peut aussi être interprétée comme un distance (élliptique) entre β^ et β^(i)~:~
Di=(β^−β^(i))′X′X(β^−β^(i))pMSE.
Alors, Di est aussi une statistique d'influence de l'unité i sur l'estimation des coefficients du modèle lin\'eaire.
Diagramme d'inflence: Avec la fonction influencePlot, on peut construire un diagramme d'influence. C'est un nuage de points des résidus contre les leviers, où le rayon du point est proportionnelle à la distance de Cook.
Pour chacune des distances de Cook donnée, nous allons calculer son rang centile selon la loi F(p,n−p). Ces unités ont aucune ou une petite influence sur l'ajustement, sauf pour l'unité 65 qui a une influence modérée.
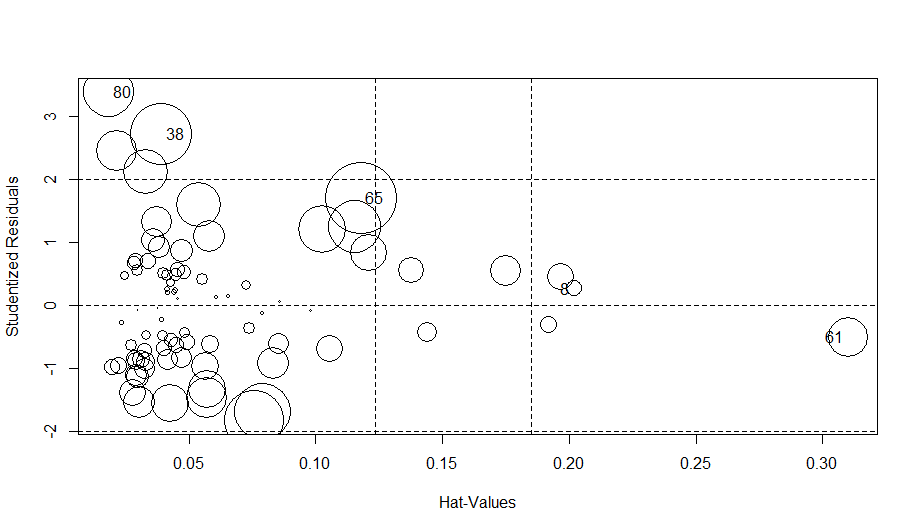
> influencePlot(mod)
StudRes Hat CookD
8 0.2676903 0.20199264 0.003672497
38 2.7294664 0.03928238 0.056157851
61 -0.5019802 0.30993906 0.022860601
65 1.7010091 0.11778952 0.075385955
80 3.3987468 0.01810318 0.037402079
> qf(influencePlot(mod)[,3],p,mod$df.residual)
[1] 0.07104867 0.23936853 0.15741165 0.27657499 0.19735371
Etudier l'influence de l'unité 65: Nous allons ajuster le modèle avec et sans l'unité 65 pour voir s'il y a des grandes différences dans les analyses. Si on
> mod<-lm(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,data=commercial)
> summary(mod)
Call:
lm(formula = Rental.Rates ~ Age + Operating.Expenses + Vacancy.Rates +
Square.Footage, data = commercial)
Residuals:
Min 1Q Median 3Q Max
-136314 -55193 -6134 40672 248457
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -521828 86089 -6.062 4.83e-08 ***
Age 38000 6641 5.722 1.98e-07 ***
Operating.Expenses 7428 1653 4.494 2.46e-05 ***
Vacancy.Rates 3755 4896 0.767 0.4455
Square.Footage 152945 73352 2.085 0.0404 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 78730 on 76 degrees of freedom
Multiple R-squared: 0.5053, Adjusted R-squared: 0.4793
F-statistic: 19.41 on 4 and 76 DF, p-value: 4.902e-11
> mod<-lm(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,data=commercial[-c(65),])
> summary(mod)
Call:
lm(formula = Rental.Rates ~ Age + Operating.Expenses + Vacancy.Rates +
Square.Footage, data = commercial[-c(65), ])
Residuals:
Min 1Q Median 3Q Max
-127948 -57914 -7982 40876 251259
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -474998 89381 -5.314 1.06e-06 ***
Age 34507 6873 5.020 3.38e-06 ***
Operating.Expenses 6905 1661 4.157 8.49e-05 ***
Vacancy.Rates 4571 4860 0.941 0.3499
Square.Footage 159337 72553 2.196 0.0312 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 77770 on 75 degrees of freedom
Multiple R-squared: 0.464, Adjusted R-squared: 0.4354
F-statistic: 16.23 on 4 and 75 DF, p-value: 1.286e-09
En alternatif, on peut utiliser une régression quantile qui est résistante aux valeurs extrêmes. Le modèle estimée est
médiane de Y=−424509,585+30254,267(age)+5013,475(frais.explotation)+6736,124(innocupation)+148814,375(superficie).
Mais, des tests d'hypothèses avec une régression quantile seront moins puissants qu'avec un modèle linéaire. Ci-bas, on observe que le modèle de régression quantile est significatif (p=5,43).
> library(quantreg)
> modQuantile<-rq(Rental.Rates~Age+Operating.Expenses+Vacancy.Rates+Square.Footage,tau=0.5,data=commercial)
> summary(modQuantile)
Call: rq(formula = Rental.Rates ~ Age + Operating.Expenses + Vacancy.Rates +
Square.Footage, tau = 0.5, data = commercial)
tau: [1] 0.5
Coefficients:
coefficients lower bd upper bd
(Intercept) -424509.585 -917198.217 -369065.151
Age 30254.267 23320.396 54799.248
Operating.Expenses 5013.475 2404.822 13356.745
Vacancy.Rates 6736.124 -11586.246 15915.648
Square.Footage 148814.375 -90941.600 338558.422
> modQuantile0<-rq(Rental.Rates~1,tau=0.5,data=commercial)
> anova(modQuantile0,modQuantile)
Quantile Regression Analysis of Deviance Table
Model 1: Rental.Rates ~ Age + Operating.Expenses + Vacancy.Rates + Square.Footage
Model 2: Rental.Rates ~ 1
Df Resid Df F value Pr(>F)
1 4 76 8.9753 5.439e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1





















 Le diagramme suggère que le lien est linéaire, mais que la variance n'est pas constante. La tension artérielle est plus variable pour les femmes plus âgées.
Le diagramme suggère que le lien est linéaire, mais que la variance n'est pas constante. La tension artérielle est plus variable pour les femmes plus âgées.


 Alternative: Référence: Applied Logistic Regression, 3rd Edition, David W. Hosmer Jr., Stanley Lemeshow, Rodney X.
(1) Construire un modèle initial d'effets principaux en utilisant des variables explicatives qui incluent les variables connues importantes et d'autres qui montrent toute évidence d'être pertinente lorsqu'elles sont utilisées comme un seul prédicteur ( par exemple, valeur-\(p < 0,\!2\) ).
Alternative: Référence: Applied Logistic Regression, 3rd Edition, David W. Hosmer Jr., Stanley Lemeshow, Rodney X.
(1) Construire un modèle initial d'effets principaux en utilisant des variables explicatives qui incluent les variables connues importantes et d'autres qui montrent toute évidence d'être pertinente lorsqu'elles sont utilisées comme un seul prédicteur ( par exemple, valeur-\(p < 0,\!2\) ).







