Introduction à R

Une introduction à R

Table des matières
Télécharger et installer R
Exemple 1 : Travailler à la console
Exemple 2 : La loi binomiale et la loi normale
Exemple 3 : Statistiques Descriptives
Exemple 4 : Fenêtre d'édition
Exemple 5 : Importer des données
Exemple 6 : Quelques diagrammes : Histogramme et diagramme à boite et moustaches.
Exemple 7 : Diagrammes à boite et moustaches comparatifs.
Exemple 8 : Opérations sur des vecteurs numériques.
Exemple 9 : Vérificatin de la normalité (histogramme)
Exemple 10 : Vérificatin de la normalité : Diagramme quantile-quantile et diagramme à l'échelle fonctionnelle normale.
Exemple 11 : Test T de Student (Une population)
Exemple 12 : Test T de Student (Mesures appariées)
Exemple 13 : Test T de Student (Populations indépendantes)
Exemple 14: Tableau de contingence
Exemple 15: Corrélation et la régression linéaire simple

Télécharger et installer R

Vidéo éducationnelle: Télécharger et installer R

A partir de votre navigateur taper R.

Télécharger R de CRAN, voir http://www.r-project.org/.
- Suivre le lien pour télécharger (download) R.
- Choisir un des sites miroirs le plus proche: Toronto.
- Choisir le système d'exploitation, par exemple Windows, Mac OS X ou Linux.
- Pour Mac, choisir la dernière version.
- Pour Windows, valider une installation pour la première fois en choisissant la base.
- Télécharger et enregistrer le fichier sur votre ordinateur.
- Ouvrir le fichier et l'exécuter
- Accepter les paramètres par défaut en cliquant successivement sur le button suivant.
- R devrait être installé avec succès.

Travailler à la Console

Vidéo éducationnelle: Travailler à la console

Sommaire de la vidéo: Voici une image de la console de R.

Nous entrons nos commandes à l'invite (c'est-à-dire après le symbole >) dans la console.

On peut utiliser R comme une calculatrice. On a calculé log(5)-2.5^2. La réponse est -4.640562. Ici log est le logarithme naturel.

> log(5)-2.5^2
[1] -4.640562

Construire des variables numériques et catégoriques avec R

Attribuer des valeurs à un vecteur avec <- ou avec =.
On peut attribuer une liste de valeurs à une variable (qui peut être numérique ou catégorique) avec la commande c().
Le c est pour combiner.

Exemple 1: Attribuer des valeurs à une variable numérique: PA (pour pression arterielle). Ici nous attribuons des valeurs à la variable PA et ensuite nous affichons le vecteur numérique PA
```
> PA = c(112, 121, 165)
> PA
[1] 112 121 165
```
Remarque: Le [1] est pour indiquer que 112 est la première valeur du vecteur.

Exemple 2: Attribuer des valeurs à une variable catégorique: nom (nom des sujets)
```
> nom = c("Alice", "Robert", Celine")
+
```
Ici il y a une erreur. Il manque des guillemets en avant de Celine. L'invite n'est pas disponible pour prendre d'autres commandes puisque R croit qu'on n'ait pas fini d'entrer la commande. On peut arrêter la commande en appuyant sur le bouton stop de la console. On peut rappeler une ancienne commande avec la flèche en haut et fixer l'erreur. On a ajouter les guillemets.
```
> nom = c("Alice", "Robert", "Celine")
```
Pour afficher les valeurs de ce vecteur, soumettre le nom du vecteur à l'invite: nom.
```
> nom
[1] "Alice"  "Robert" "Celine"
```
Exemple 3: Enlever un vecteur de la session de travail.
- On peut utiliser la fonction ls() pour donner ou afficher une liste de tous les vecteurs utilisés pendant la session de travail.
```
> ls()
[1] "nom" "PA"
```
- On peut aussi enlever ou effacer des vecteurs avec fonction rm(). Ici on enlève le vecteur nom.
```
> rm(nom)
> ls()
[1] "PA"
```

La loi binomiale et la loi normale

Vidéo éducationnelle: La loi binomiale et la loi normale

Sommaire de la vidéo:

NB : Le symbole # est utilisé pour écrire des commentaires avec R. R n'interprète pas les commentaires.

Voici un exemple d'un commentaire :

 > # J'étudie la biostatistique

Voici des exemples d'évaluation de probabilités avec la loi binomiale.

Binomiale:

Avec R, le nom de la loi binomiale est binom. Un préfixe d ou p est utilisé avec le nom binom.

dbinom est la loi de probabilité. Son utilisation est dbinom(x, size, prob), où x est une valeur dans l'image de la variable aléatoire, size est le nombre d'épreuves et prob la probablité du succès.
Exemple: Calculons P(X=20), où Xsuit une loi binomiale avec n=30 et p=0,75.

Solution: On a P(X=20)=0.0909. Voici le calcul avec R.
```
> dbinom (20, 30, 0.75)
[1] 0.09086524
```
Ce n'est pas nécessaire d'indiquer "size=" et "prob=" si on met les arguments dans le bon ordre:
```
        > dbinom(20,30,.75)
        [1] 0.09086524
       
```
pbinom est la fonction de répartition. Son utilisation est pbinom(x, size, prob), où x est un nombre, size est le nombre d'épreuves et prob la probablité du succès.
Calculons P(X ≤20). On veut P(X ≤20)=F(20)=0,1966. Voici le calcul avec R.
```
	> pbinom(20,30,0.75)
	[1] 0.1965934
       
```
Calculons P(20 ≤X ≤25). On peut calculer P(X=x) pour x=20,21,...,25:
```
	
	> dbinom(20:25,30,0.75)
	[1] 0.09086524 0.12980749 0.15930919 0.16623567 0.14545621 0.10472847
        
```
Mais on veut la somme de ces probabilités, alors on utilise la commande sum:
```
	> sum(dbinom(20:25,30,0.75))
	[1] 0.7964023
       
```
Alors, P(20 ≤X ≤25)=0,7964. Commentaire: Une autre façon d'obtenir cette probabilité est d'utiliser la fonction de répartition. On veut P(20 ≤X ≤25)=P(X ≤25)-P(X≤19)=F(25)-F(19)=0,7964. Voici le calcul avec R.
```
	> pbinom(25,30,0.75)- pbinom(19,30,0.75)
	[1] 0.7964023
       
```

Sommaire pour la loi Binomiale: On utilise un préfixe de p pour la fonction de répartition et un préfixe de d pour obtenir la loi de probabilité.

La loi normale: Supposons qu'on veut travailler avec une certaine loi normale.

Le nom avec R de la loi normale est norm.
On utilise le préfixe p pour la fonction de répartition.
On utilise le préfixe q pour la fonction quantile.

Voici des exemples. Supposons que X suit une loi normale de moyenne 25 et d'écart type 5,25.

Calculons P(X<20). On veut P(X<20)=F(20) =0,1705. Voici le calcul avec R.
```
	> pnorm(20,25,5.25)
	[1] 0.1704519
       
```
Calculons P(20 < X <25). On veut P(20 < X <25)=F(25)-F(20)=0,3295. Voici le calcul avec R.
```
	> pnorm(25,25,5.25) - pnorm(20,25,5.25)
	[1] 0.3295481
        
```

Fonction Quantile: Le préfixe est q pour la fonction quantile. Voici des exemples.

On veut le 5ème centile, c'est-à-dire une valeur q tel que P(X. Le premier argument sera 0.05 pour le 5ième quantile et les autres arguments seront la moyenne (ici c'est 25) et l'écart type (ici c'est 5.25). Alors, le 5ième quantile est q=16,3645. Voici le calcul avec R.
> qnorm(0.05,25,5.25) [1] 16.36452
Supposons que l'on veut obtenir le 95ième centile, qui est 33,6355. C'est-à-dire on veut une valeur q tel que P(X > qnorm(0.95,25,5.25) [1] 33.63548
Supposons que l'on veut calculer le premier quartile (qui est 21,46 environ) et le troisième quartile (qui est 28,54 environ). C'est-à-dire, on veut le 25ième centile et le 75ième centile. On utilise :
> qnorm(0.25,25,5.25) [1] 21.45893 > qnorm(0.75,25,5.25) [1] 28.54107
Supposons qu'on aimerait calculer la distance inter quartile. C'est la distance entre le troisième quartile et le premier quartile. On utilise :
> qnorm(0.75,25,5.25) - qnorm(0.25,25,5.25) [1] 7.082142

Sommaire pour la loi normale: Le nom avec R pour la loi normale est norm. On utilise le préfixe p pour la fonction de répartition et le préfixe de q pour obtenir des quantiles.

Statistiques Descriptives

Vidéo éducationnelle: Statistiques Descriptives

Sommaire de la vidéo:

Soit x une variable numérique déjà défini avec R, la commande ls() permet d'afficher les objets qu'on ait déjà défini durant cette session. Nous observons qu'il y a un objet nommé x. Nous allons afficher x.
> x [1] 12 13 11 9 2 75 125 35

Remarque: Nous avions construit ce vecteur avec la commande: x=c(12, 13, 11, 9, 2, 75, 125, 35)

Utiliser is.numeric(x) pour savoir si x est numérique.
Utiliser is.vector(x) pour vérifier si c'est un vecteur.
Avec un vecteur numérique, on peut calculer des statistiques descriptives.
La fonction length permet de calculer la longueur du vecteur (c'est-à-dire le nombre de composantes) :
> length(x) [1] 8
Notre vecteur numérique a 8 composantes.
La fonction summary nous donne un sommaire de plusieurs statistiques descriptives.
> summary(x) Min. 1st Qu. Median Mean 3rd Qu. Max. 2.00 10.50 12.50 35.25 45.00 125.00

Voici quelques commandes pour obtenir certaines statistiques descriptives.
mean(x) # pour la moyenne median(x) # pour la médiane var(x) # pour la variance sd(x) # pour l'écart type IQR(x) # pour la distance interquartile range(x) # pour l'étendue (permet d'afficher le min et le max) range(x)[2] - range(x)[1] # pour la différence entre le max et le min sort(x) # pour ordonner les valeurs en ordre croissant

quantile(x) # pour quelques centiles
> quantile(x) 0% 25% 50% 75% 100% 2.0 10.5 12.5 45.0 125.0
Remarques :
Ici, le 25ième et 75ième centile sont le premier et le troisième quartile. Le premier quartile est 10,5, le troisième quartile est 45, et le 50ième centile (qui est la médiane) est 12,5.
Il y a plusieurs façons de calculer les quartiles. Si nous voulons des quartiles en utilisant la formule qu'on ait apprise en classe, utiliser quantile(x,type=6). On obtient
> quantile(x,type=6) 0% 25% 50% 75% 100% 2.0 9.5 12.5 65.0 125.0
Alors, q1=9,5 et q3=65.
On peut aussi changer l'ordre de nos centiles. Supposons que nous voulons le 5ième centile et le 95ième centile:
> quantile(x, c(0.05, 0.95)) # pour obtenir le 5ième et le 95ième centile

On utilise la commande boxplot(x) pour créer un diagramme à boites et moustaches de la variable x.
On utilise boxplot(x)$out pour obtenir les valeurs aberrantes.

Fenêtre d'édition

Vidéo éducationnelle: Fenêtre d'édition

Sommaire de la vidéo:
Pour travailler avec R, nous pouvons entrer directement des commandes à l'invite dans la console de R.

Supposons que l'on veut créer un vecteur numérique w. Avec la fonction c, on peut attribuer des valeurs à w. Ci bas, avec R, nous avons attribué des valeurs au vecteur numérique w et nous affichons des statistiques descriptives pour w avec la fonction summary.
> w = c(12,25,36,47,23,11,10) > summary(w) Min. 1st Qu. Median Mean 3rd Qu. Max. 10.00 11.50 23.00 23.43 30.50 47.00

En alternative, au lieu d'utiliser la console, c'est souvent plus efficance d'entrer les commandes dans une fenêtre d'édition avec R.
Dans R GUI Choisir File -> New Script (en Windows) ou File -> New Document (sur un Mac).
On entre nos commandes dans la fenêtre d'édition et ensuite on sélectionne les commandes pour les soumettre à la console.

Voici un exemple. Voici des commandes que nous avons inscrites dans une fenêtre d'édition :
## y est une variable numérique y = c(12,45,67,49,29,23,67) boxplot(w,y)
Pour soumettre les commandes à la console, on sélectionne les commandes qu'on veut soumettre et on utilise CTRL-R (sur windows) ou CMD-Enter (avec un Mac). Ensuite, quand nous allons dans la console, on voit le résulat:
> ## y est une variable numérique > y = c(12,45,67,49,29,23,67) > boxplot(w,y)
R va aussi avoir construit des diagrammes à boite et moustaches comparatifs dans une fenêtre graphique.
Remarques :
On utilise le symbole # pour des commentaires. R va ignorer tout ce qui vient après le symbole #.
Nous pouvons sauvegarder les commandes dans la fenêtre d'édition. Maximiser la fenêtre d'édition, et choisir file et save as. Le fichier devrait avoir l'extension (.R). Voici un exemple : RStuff.R

Importer les données d'une fichier

Vidéo éducationnelle: Importer des données d'une fichier.

Sommaire de la vidéo:

Nous allons importer des données à partir d'un fichier texte délimité par des tabulations. Nous pouvons construire un fichier texte délimité par des tabulations avec une feuille de travail d'Excel ou d'Open Office Calc (qui est gratuit).
Les colonnes sont les variables. Les rangés sont les unités statistiques.
Dans notre premier exemple, nous avons des paires mère-fille qui sont les unités statistiques. Nous allons utiliser deux variables numériques pour décrire les unités: la taille de la mère en cm et la taille de la fille en cm. Nous avons sauvegardé le jeu de données en tant que fichier texte délimité par des tabulations nommé MereFille.txt. [Faites un clic droit sur le fichier et SAUVEGARDER SOUS (avec un Mac essayer deux doigts avec le clic de la souris et SAUVEGARDER SOUS)].
Avec R, utilisez la fonction read.table pour importer des données à partir d'un fichier texte. R va créer un jeu de données dit dataframe.
Dans l'exemple ci-dessous, nous importons les données du fichier MereFille.txt. Nous appellons le jeu de données donnees.
> donnes = read.table(file.choose(), header=TRUE, sep="\t")

N.B. : donnes est le nom que nous avons donné au jeu de données.

Arguments:

file.choose() : Avec cet argument, R va ouvrir une fenêtre pour nous permettre de trouver notre fichier.

header=TRUE: Par défaut, R suppose que nous n'avons pas donné de noms aux colonnes. C'est-à-dire que la premier unité statistique dans la première rangé. Mais, nous préférons donner des noms aux colonnes. Pour donner des noms aux colonnes, on met les noms des colonnes dans la première rangé du fichier. Alors, cet argument indique à R que la première rangé contient les noms des colonnes.

sep="\t": Par défaut, R utilise des espaces pour délimiter les colonnes. Nous avons utiliser des tabulations pour délimiter les colonnes, alors on indique ceci avec l'argument sep="\t".
Lorsque la commande est entrée, une fenêtre est ouverte afin que nous puissions rechercher le fichier. Sélectionnez le fichier et cliquez sur open . Maintenant, les données ont été importées avec R.

Travailler avec un jeu de données (dataframe) ...

Nous pouvons vérifier que données est un data frame.
> is.data.frame(donnees) [1] TRUE
R affiche TRUE, alors donnees est un data frame, c.-à-d. un tableau où les unités statistiques sont dans les rangés et les variables sont dans les colonnes.
On utilise la fonction names pour afficher les noms des colonnes. Ci-bas, on affiche les noms des colonnes pour le dataframe donnees :
> names(donnees) [1] "Fille" "Mere"
On observe deux colonnes nommées : "Fille" et "Mere".
Pour accèder une colonne dans un dataframe, on utilise le nom du dataframe avec un signe de dollar et ensuite le nom de la colonne. Ci-bas, on affiche la colonne "Fille" du dataframe donnees :
> donnees$Fille [1] 160 165 156 169 152 156 162 156 161 160 164 162
On peut aussi référer à la colonne en utilisant son indice au lieu de son nom.
> donnees[,1] [1] 160 165 156 169 152 156 162 156 161 160 164 162
On utilise des paranthèses carrées pour utiliser des indices. Ici nous avons utiliser [,1] pour obtenir toutes les rangés, mais seulement la première colonne. Ci-bas, on affiche la deuxième colonne du donnees
> donnees[,2] [1] 163 165 162 161 161 160 164 159 164 161 163 168
La deuxième colonne est appelée "Mere", donc ici, nous utilisons le nom pour accéder à la 2ème colonne :
> donnees$Mere [1] 163 165 162 161 161 160 164 159 164 161 163 168

Ici nous utilisons la fonction summary pour afficher quelques statistiques descriptives pour la taille des mères (en cm).
> summary(donnees$Mere) Min. 1st Qu. Median Mean 3rd Qu. Max. 159.0 161.0 162.5 162.6 164.0 168.0
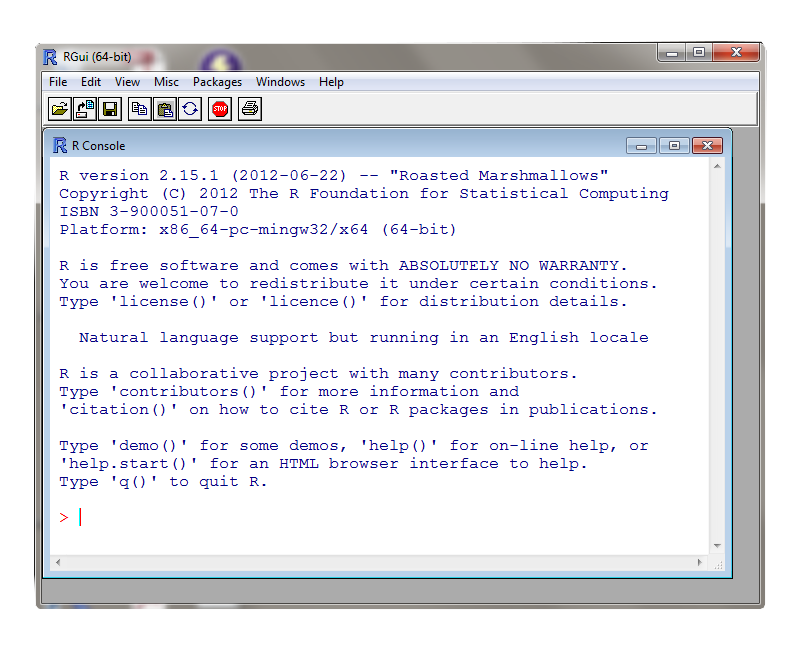
Ici nous utilisons la fonction boxplot pour afficher des diagrammes à boites et moustaches comparatifs des tailles des mères et des tailles des filles.
> boxplot(donnees$Mere,donnees$Fille,names=c("Mères","Filles"))
Voici le diagramme :

Voici un deuxième exemple. Dans notre feille de travaille Excel, les rangés sont les unités statistiques qui sont des pommes de laitues. Nous allons décrire les unités avec deux variables : une variable numérique qui est la masse sèche de la laitue et une variable catégorique qui identifie si la laitue fut en compétition. La laitue fut en compétition avec de l'épinard ou elle ne fut pas en compétition.
On a sauvegardé les données dans un fichier texte délimité par des tabulations. Le nom du fichier est laitue.txt.
Avec R, on utilise la fonction read.table pour importer les données du fichier texte. Ceci va créer un dataframe (jeu de données) avec R. Dans l'exemple suivant, nous importons des données du fichier suivant : laitue.txt.
> laitue = read.table(file.choose(), header=TRUE, sep="\t")
On nomme le jeu de données laitue.
On affiche les noms des colonnes :
> names(laitue) [1] "masse.sec" "en.concurrence"
Il y a deux colonnes. En outre, remarquons que R a mis un point dans le nom "masse.sec". R va substituer des symboles (comme l'espace) qui ne sont pas permis dans le noms des variables par un point.
Ci bas, on calcul la moyenne de la masse sèche pour toutes les pommes de laitues.
> mean(laitue$masse.sec) [1] 2.750667
Nous avons deux groupes de laitues, les laitues en compétition avec l'épinard et les laitues qui ne sont pas en compétition. On calcul la moyenne de la masse sèche pour chaque groupe avec la fonction aggregate et une notation de formule.
> aggregate(masse.sec~en.concurrence, laitue,mean) en.concurrence masse.sec 1 non 3.020 2 oui 2.212

Arguments:

Dans le premier argument, on utilise une notation de formule pour indiquer qu'on veut "masse.sec" selon les niveaux de la variable "en.concurrence".
Dans le deuxième argument, on a le nom du dataframe. Dans notre cas, c'est laitue.
Dans le troisième argument, on donne la nom de la fonction que R doit évaluer. Dans notre cas, on veut la moyenne (qui est mean avec R) pour chaque groupe.
Voici l'écart type de la masse sèche pour chaque groupe.
> aggregate(masse.sec~en.concurrence, laitue,sd) en.concurrence masse.sec 1 non 0.9350325 2 oui 0.7774531

Si nous voulons faire référence à un des sous-groupes, on peut demander à R de vérifier une condition. Voici un exemple où nous référons à la masse sèche des laitues en compétition. On commence avec un affichage des niveaux de la variable catégorique en.concurrence.
> levels(laitue$en.concurrence) [1] "non" "oui"
Nous allons calculer la moyenne de la masse sèche des laitues en compétition, c'est-à-dire pour le groupe "oui". En utilisant les parenthèses carrées, on demande à R de vérifier pour chaque rangé si la condition dans la parenthèse est satisfaite. Si la condition n'est pas satisfaite, alors R ignore cette rangé.
> mean(laitue$masse.sec[laitue$en.concurrence=="oui"]) [1] 2.212
On peut aussi utiliser la notation de formule avec la fonction boxplot.
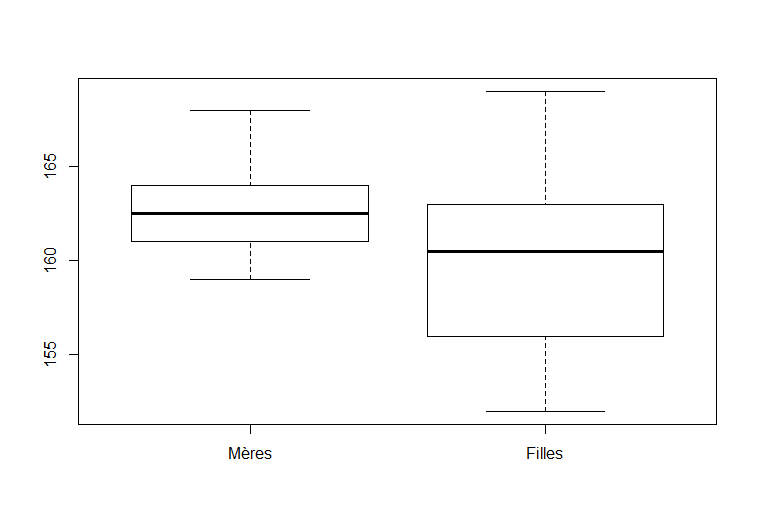
> boxplot(masse.sec~en.concurrence,laitue)
La commande ci-haut produit des diagrammes à boites et moustaches comparatifs pour la masse sèche selon le niveau de la concurrence. Voici le diagramme :

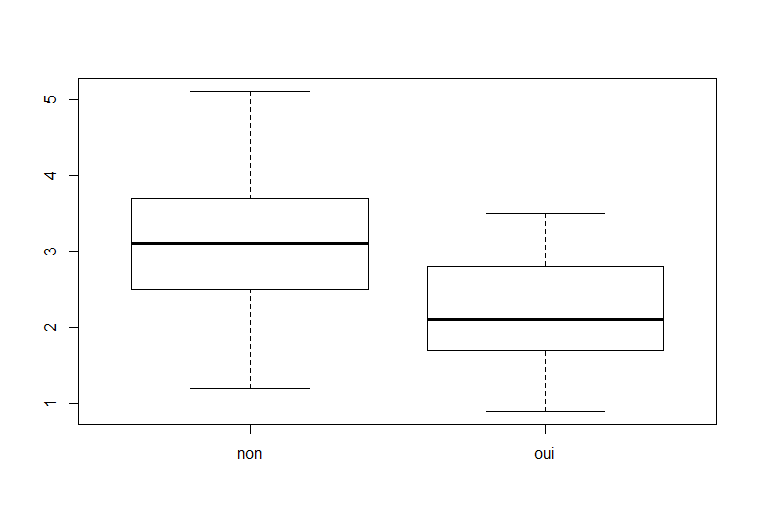
Mots clés : read.table, indices, boxplot, summary, aggregate

Quelques diagrammes: histogramme et diagramme à boites et moustaches

Vidéo éducationnelle: Histogramme et diagramme à boite et moustaches

Sommaire de la vidéo:

Supposons que x est un vecteur numérique. Pour construire un histogramme de x, on utilise la commande hist(x) et pour un diagramme à boite et moustaches, on utilise la commandes boxplot(x).
Pour notre exemple, nous allons importer les données du fichier TEMPSDESURVIE.txt en utilisant la fonction read.table.
> donnees = read.table(file.choose(),header=TRUE,sep="\t") > names(donnees) [1] "Temps.de.survie..en.mois."
Remarques:
Nous avons créé un jeu de données (un dataframe) avec R. Ce jeu de données est nommé donnees et le jeu de données contient une colonne qui est nommée "Temps.de.survie..en.mois.".
Pour référer à cette colonne, on utilise donnees$Temps.de.survie..en.mois.
Pour voir le nombre de colonne et le nombre de rangés, on utilise:
> ncol(donnees) [1] 1 > nrow(donnees) [1] 250
Alors, le jeu de donnees a une colonne et 250 rangés (pour les 250 patients).

La commande pour construire l'histogramme pour le temps de survie est
> hist(donnees$Temps.de.survie..en.mois.)
Voici le résultat.
On peut changer l'étiquette sur l'axe verticale avec ylab, sur l'axe horizontale avec xlab et changer le titre avec main. Considérons la commande suivante :
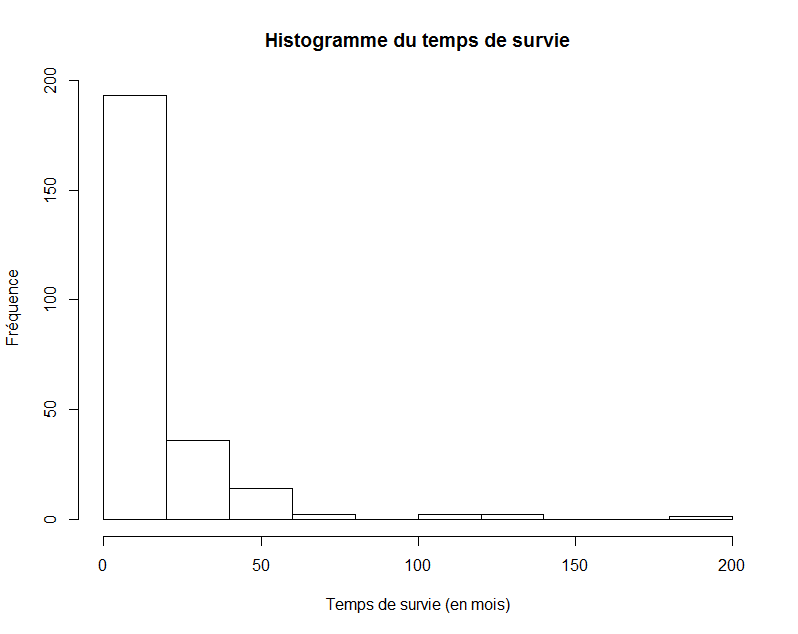
hist(donnees$Temps.de.survie..en.mois.,ylab="Fréquence", xlab="Temps de survie (en mois)",main="Histogramme du temps de survie")
Voici le résultat.
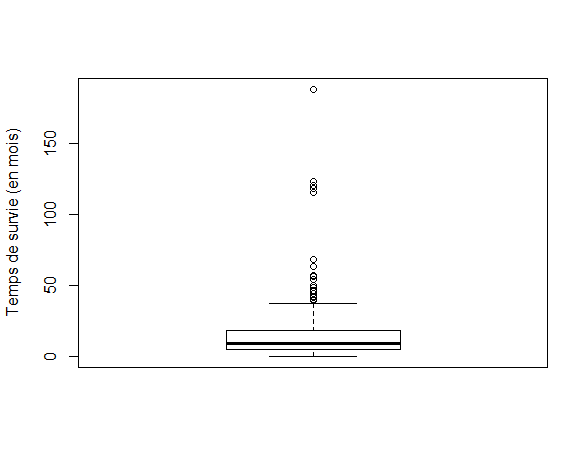
On peut constuire un diagramme à boite et moustache avec la fonction boxplot. Considérons la commande suivante :
> boxplot(donnees$Temps.de.survie..en.mois.,ylab="Temps de survie (en mois)")
Voici le résultat. Remarque: R calcul les quartiles d'une façon différente que nous. Notre formule pour les quartiles est les quantiles de type 6 avec R. Nous avons défini une fonction avec R qui nous permet de construire un diagramme à boite et moustaches avec des quantiles de type 6. La fonction est dans le fichier plots.r. Sauvegarder ce fichier. Pour utiliser cette fonction, il faut ouvrir le fichier avec R de la façon suivante:
> source(file.choose())
R va ouvrir une fenêtre et sélectionner le fichier plots.r. Pour vérifier que vous avez bien ouvert le fichier, considérer la commande suivante:
> BoxPlot function(x, ...) UseMethod("BoxPlot")
Si vous voyez function(x, ...) UseMethod("BoxPlot"), après avoir entrer BoxPlot à l'invite, alors vous avez accès à la fonction BoxPlot. On utilise la fonction BoxPlot comme la fonction boxplot. Mais, BoxPlot utilise des quantiles de type 6.
Mots clés: histogramme, diagramme à boite et moustaches, quantile de type 6.

Diagrammes à boite et moustaches comparatifs.

Vidéo éducationnelle: Diagrammes à boîte et moustaches comparatifs

Sommaire de la vidéo:

On considère deux façons d'utiliser la fonction boxplot (i) nous avons les données dans des vecteurs numériques différents; (ii) nous avons importé les données d'un fichier et nous avons construit un jeu de données (dataframe) avec ces données.
Pour notre premier exemple, nous supposons que nous avons au moins deux groupes de valeurs numériques que nous voulons comparer. Pour notre exemple, nous avons trois groupes. Nous allons construire un vecteur pour chacun des groupes.
> x=c(12,13,24,56,100,45,67,45,34,23) > y=c(11,14,24,57,115,65,67,45,34,24) > z=c(12,34,56,34,99,98,65,34,23,11,10,9,23,65)
Nous utilisons des diagrammes à boite et moustaches comparatifs avec la fonction boxplot.
> boxplot(x,y,z)
Remarque: R va nommer les groupes 1, 2, et 3, respectivement. Nous allons modifier les noms des groupes avec l'argument names. On peut aussi donner une étiquette à l'axe vecticale en utilisant l'argument ylab. Voici la commande que nous avons utiliser pour construire le diagramme ci bas.
boxplot(x,y,z,names=c("Groupe 1","Groupe 2","Groupe 3"), ylab="Taille (en cm)")

R calcul les quartiles en utilisant une différente formule que nous. Notre formule est équivalente à un quantile de type 6 avec R. Nous avons défini une fonction avec R qui construit les diagrammes à boite et moustaches avec des quantiles de type 6. La fonction est dans le fichier plots.r. Sauvegarder le fichier, nous allons importer le fichier en utilisant la commande suivante avec R.
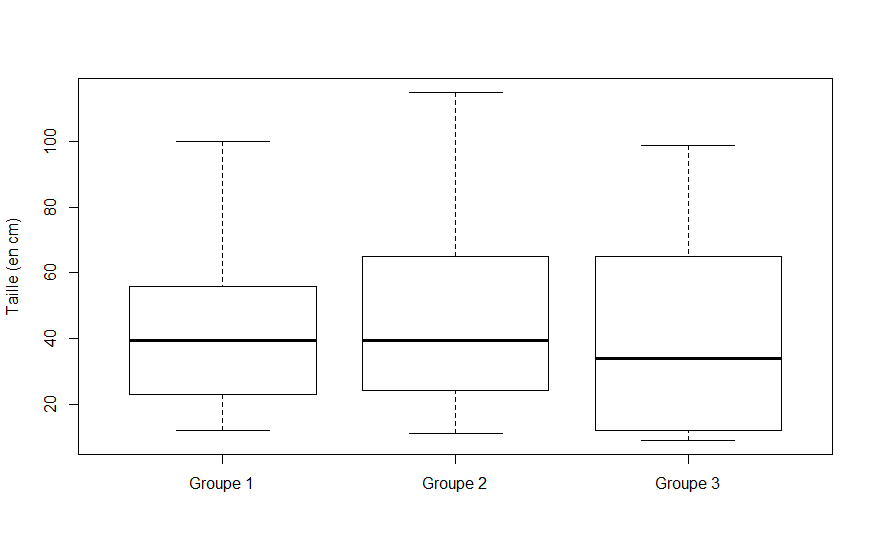
> source(file.choose())
R va ouvrir une fenêtre et nous allons sélectionner le fichier plots.r. Pour vérifier que nous avons bien importer le fichier, utilisez la commande suivante :
> BoxPlot function(x, ...) UseMethod("BoxPlot")
Si vous voyez function(x, ...) UseMethod("BoxPlot"), après avoir soumis la commande BoxPlot à l'invite, alors, vous avez maintenant accès à la fonction BoxPlot. On peut utiliser BoxPlot exactement comme la fonction boxplot. Mais, BoxPlot utilise les quantiles de type 6.
Pour notre prochain exemple, nous allons importer les données du fichier texte : weather2007.txt. On commence avec l'attribution des données à un jeu de données avec la fonction read.table.
> donnees = read.table(file.choose(),header=TRUE,sep="\t")
Remarques:
Un jeu de données est un tableau de valeurs. Les rangés sont les unités statistiques (ici un unité est une journée en 2007). On peut afficher le nombre de rangés.
> nrow(donnees) [1] 365
On voit qu'il y a une rangé pour chacune des 365 journées de l'année 2007. On utilise des variables pour décrire les unités. Les variables sont dans les colonnes. L'argument header=TRUE est utilisé pour indiquer à R que dans la première rangé du fichier, nous avons les noms des colonnes. On utilise names pour afficher les noms des colonnes.
> names(donnees) [1] "Avg.Temp...C." "Avg.Temp...F." "Avg.Wind..mph." "Precip..in." "Day" "Month" [7] "Season"
On observe 7 colonnes.

Supposons que nous avons un vecteur numérique y et un vecteur catégorique x (pour identifier les groupes) dans le jeu de données donnees. Pour construire des diagrammes à boîte et moustaches comparatifs pour y selon les niveaux de x, on utilise
boxplot(y~x,donnees)

Nous allons construire des diagrammes à boîtes et moustaches comparatifs de la vitesse moyenne du vent selon le mois.
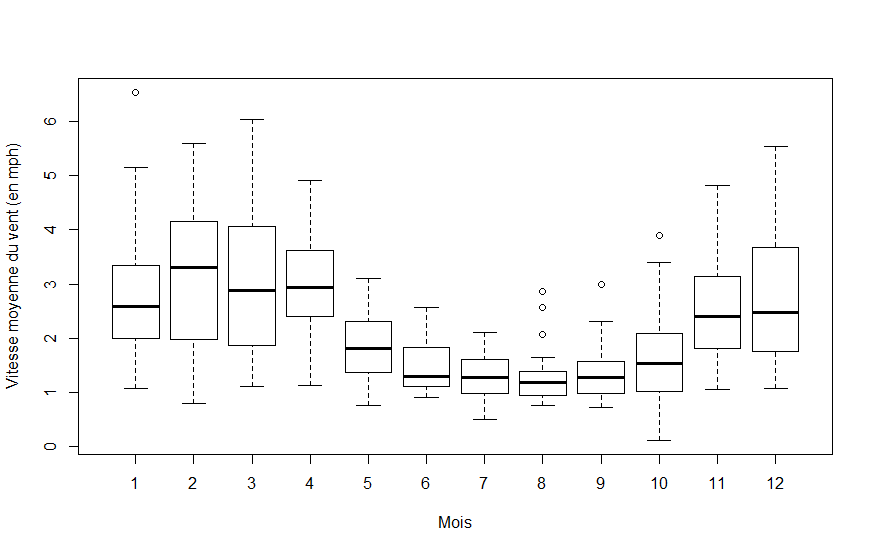
boxplot(Avg.Wind..mph.~Month,donnees)
On ajoute des étiquettes aux axes avec ylab et xlab. Voici la commande et le diagramme correspondant.
BoxPlot(Avg.Wind..mph.~Month,donnees,ylab="Vitesse moyenne du vent (en mph)",xlab="Mois")
Remarque: Si nous avons importer le fichier plots.r, avec la commande source(file.choose()), alors nous pouvons utiliser la fonction BoxPlot de la même façon que la fonction boxplot sauf que les quartiles sont des quantiles de type 6.
BoxPlot(Avg.Wind..mph.~Month,data,ylab="Average Wind Speed (in mph)",xlab="Month")

Vérification de la normalité : Diagramme quantile-quantile et diagramme de probabilité à l'échelle normale.

Vidéo éducationnelle: Diagramme quantile-quantile

Sommaire de la vidéo:
Considérons les trois vecteurs numériques suivants. Pour chacun, est-ce raisonnable de supposer que c'est un échantillon aléatoire d'une population normale? En d'autres mots, on veut vérifier la condition de normalité.
x=c(15.0, 15.3, 16.1, 5.4, 14.7, 14.7, 14.6, 13.8, 14.0, 14.6, 16.3, 18.6, 15.3, 15.3, 15.7, 10.7, 12.9, 15.3, 13.7, 14.1, 13.7,14.8, 16.8, 16.2, 16.0) y=c(11.7, 9.4, 11.0, 9.6, 6.2, 7.4, 12.6,8.2, 9.1, 9.7, 9.6, 11.6, 9.5, 12.1,10.2, 6.1, 11.8, 9.6, 7.4, 10.4) w=c(30.1, 30.1, 37.8, 38.3, 34.5, 31.9, 41.2,30.3, 30.0, 30.1, 34.7, 30.8, 30.7, 33.4,30.7, 30.2, 34.0, 33.7, 31.9, 30.7)

Nous allons utiliser la fonction qqnorm pour constuire un diagramme quantile-quantile pour vérifier la normalité. Les commandes suivantes nous donne un diagramme quantile-quantile pour y et superimpose une droite sur le diagramme. L'ordonnée à l'origine de la droite est la moyenne et la pente est l'écart type.
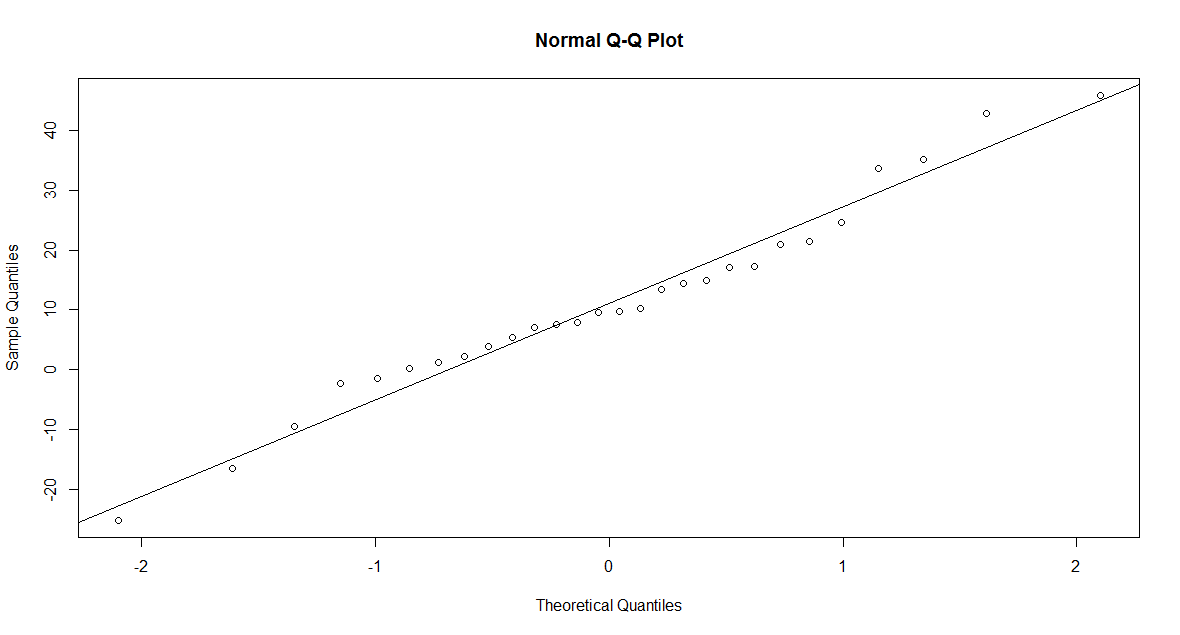
> qqnorm(y) > abline(mean(y),sd(y))
Voici le diagramme quantile-quantile correspondant. Il y a une tendance linéaire dans le diagramme avec un petit écart aux extrémités. Alors, c'est raisonnable de supposer que c'est un échantillon d'une population normale. Remarques:
Nous allons expliquer approximativement la construction du diagramme. A l'axe vertical, nous avons les quantiles de l'échantillons (c-à-d. les n observations). Chaque observations a un rang centile. Avec le rang centile, on trouve le quantile correspondant d'une loi normale centrée et réduite. Considérons les statistiques descriptives suivantes pour y.
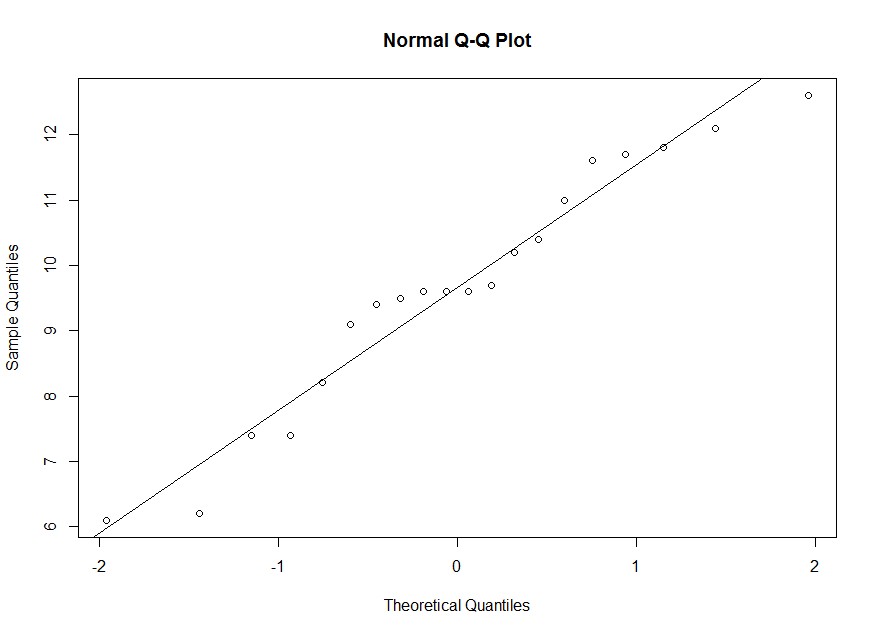
> summary(y) Min. 1st Qu. Median Mean 3rd Qu. Max. 6.100 8.875 9.600 9.660 11.150 12.600
Le 50ième centile de l'échantillon est 9,66. Mais le 50ième centile pour une variable normale centrée et réduite est z=0. Alors, on fait une correspondance entre 9,66 sur l'axe verticale et 0 sur l'axe horizontale. Le 25ième centile de l'échantillon est 8,875. Mais le 25ième centile pour une variable normale centrée et réduite est z=-0,674. Alors, on fait une correspondance entre 8,875 sur l'axe verticale et -0,674 sur l'axe horizontale. Et ainsi de suite.
> qnorm(0.25,0,1) [1] -0.6744898

Si nous avons un échantillon d'une population normale, alors nous devrons espérer voir une tendance linéaire dans le diagramme (avec une possibilité d'un petit écart aux extrémités). Si nous n'observons pas une tendance linéaire dans le diagramme, alors ce n'est pas raisonnable du supposer que le vecteur numérique est un échantillon d'une population normale.
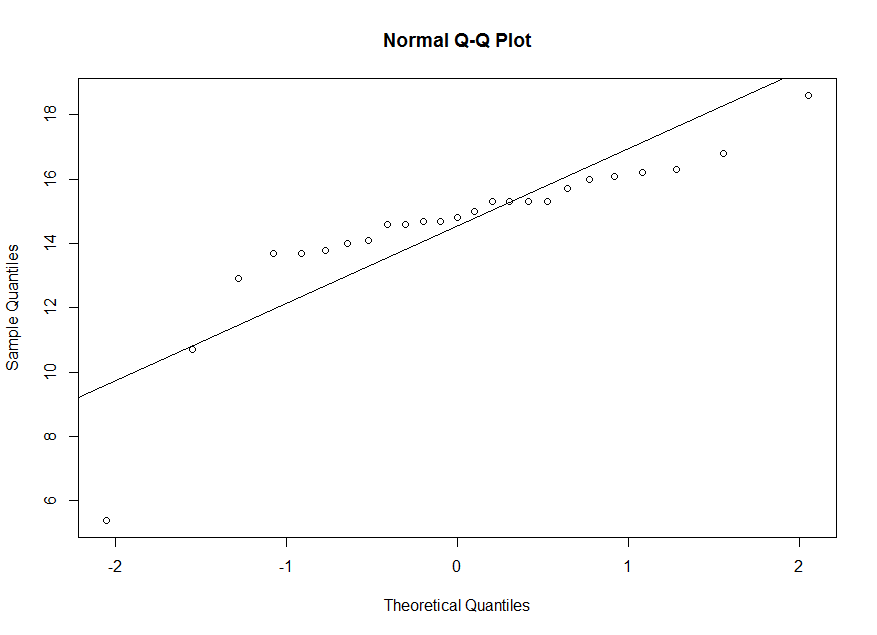
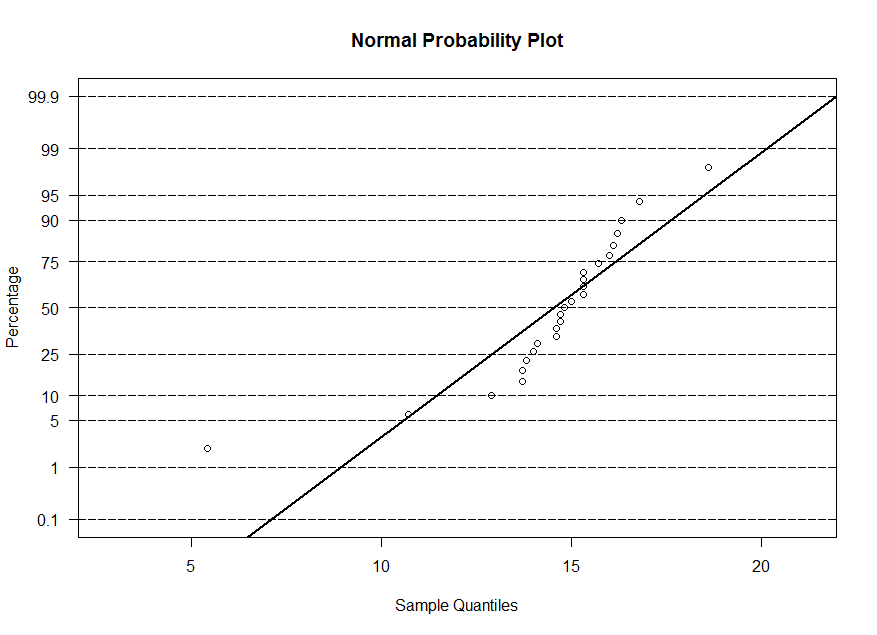
Voici les commandes pour constuire un diagramme quantile-quantile pour x. On observe une déviation de la droite. Alors, ce n'est pas raisonnable de supposer que x est un échantillon aléatoire d'une population normale.
> qqnorm(x) > abline(mean(x),sd(x))

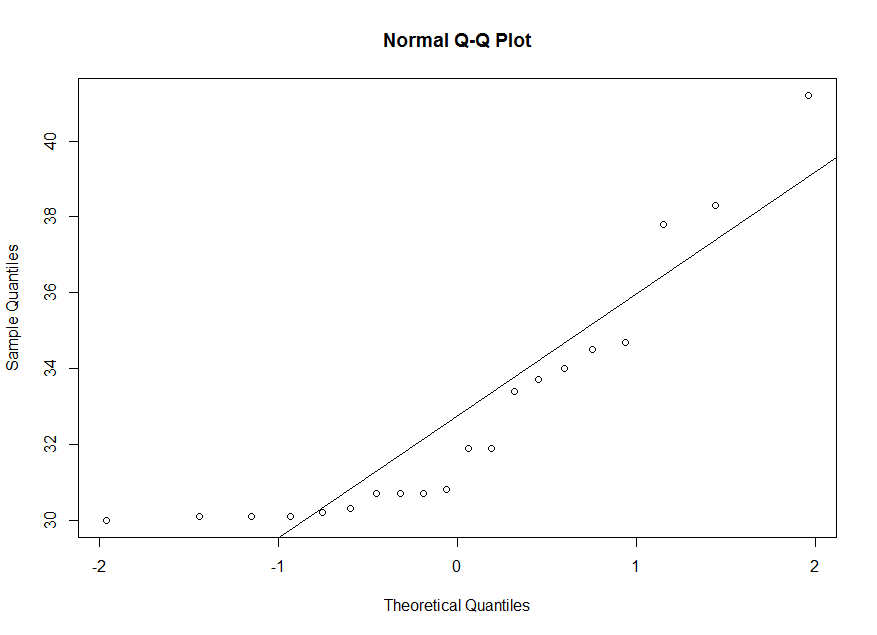
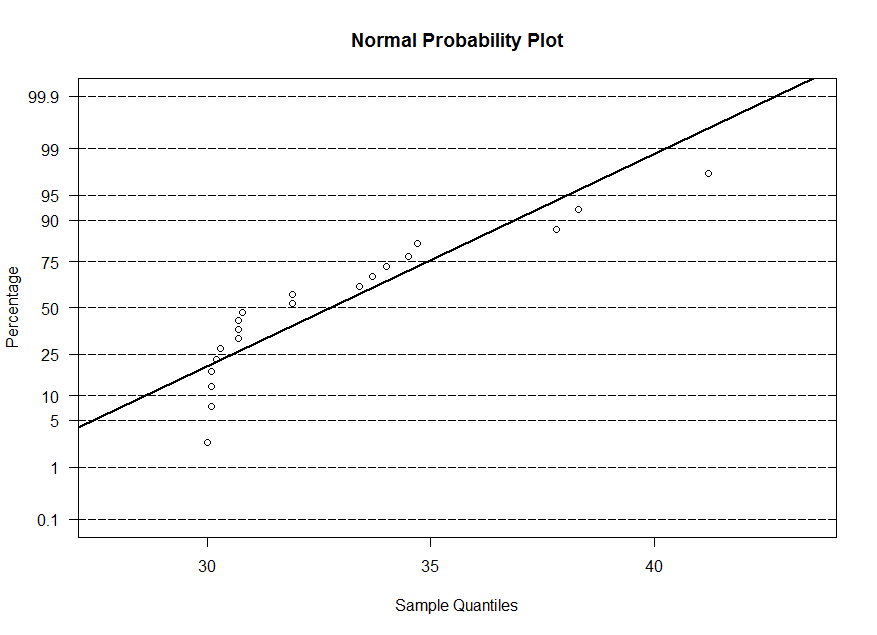
Voici les commandes pour construire un diagramme quantile-quantile pour w. On observe une tendance curviligne dans le diagramme. Alors, ce n'est pas raisonnable de supposer que w est un échantillon d'une population normale.
> qqnorm(w) > abline(mean(w),sd(w))
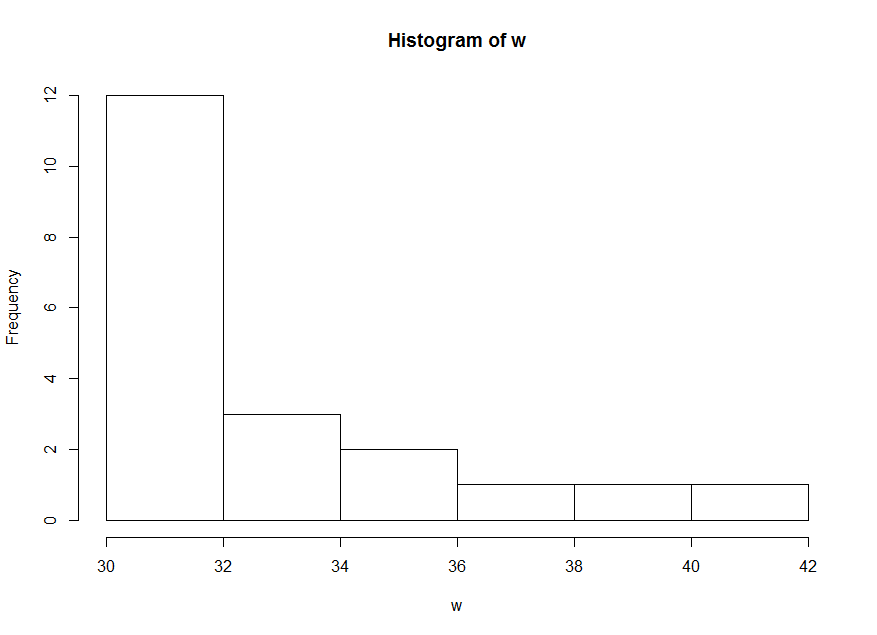
De son histogramme, on observation que la distribution de w a une très grande asymétrie positive.

Considérons les données dans le fichier texte suivant : methadone.txt. Nous attribuons les données au jeu de données qu'on nomme
donnees
et nous affichons les noms des colonnnes. Il y a trois colonnes. La première est une variable d'identification du patient. Les deux autres sont des scores de douleurs pour le patient sous le placébo et sous la méthadone. Alors, chaque patient a deux scores de douleurs. On calcul la différence entre les deux scores de douleurs et on produit un diagramme quantile-quantile pour cette différence.
> donnees=read.table(file.choose(),header=TRUE,sep="\t") > names(donnees) [1] "patient" "placebo" "methadone" > d=donnees$placebo-donnees$methadone > qqnorm(d) > abline(mean(d),sd(d))
Voici le diagramme quantile-quantile pour la différence des scores de douleurs. Il y a une tendance linéaire dans le diagramme. Alors, c'est raisonnable de supposer que la différence entre les scores de douleurs est normalement distribuée.
R n'a pas de fonction dans la base pour construire un diagramme de probabilité à l'échelle normale. Mais, nous avons écrit une fonction pour vous. Elle est dans le fichier plots.r. Nous allons importer ce fichier. Le fichier contient la fonction ppnorm.

Avec la commande suivante, nous allons importer le fichier
plots.r
et vérifier que le fichier fut bien importé en utilisant la commande ppnorm.
> source(file.choose()) > ppnorm function(x, ...) UseMethod("ppnorm")
Remarque : Si nous avons bien importé le fichier plots.r, alors on devrait voir function(x, ...) UseMethod("ppnorm"), après avoir entrer la commande
ppnorm
à l'invite. L'utilisation de la fonction est ppnorm(x), où x est un vecteur numérique.
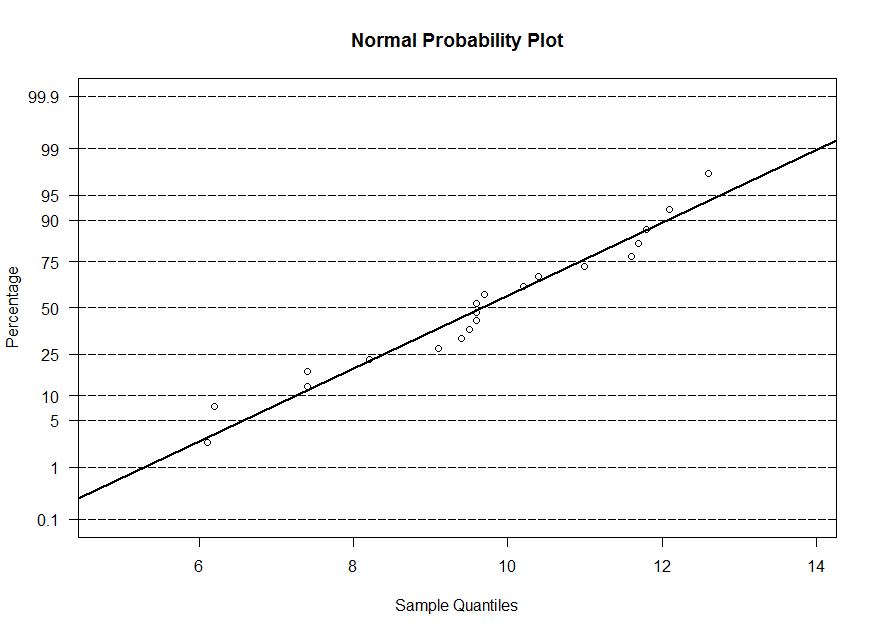
Voici les diagrammes de probabilité pour x, y et w. Le diagramme à probabilité à l'échelle normale est semblable au diagramme quantile-quantile, mais les quantiles de l'échantillon sont à l'axe horizontale et les quantiles théoriques sont à l'axe verticale (en outre on affiche la probabilité au lieu de la valeur du z, on a 50% à z=0 et 95% à z=1,645). Alors, les diagrammes sont équivalents. Mais la droite superimposée utilise -(moyenne/écart type) pour l'ordonnée à l'origine et 1/(écart type) pour la pente.
> ppnorm(x)

> ppnorm(y)

> ppnorm(w)

Comparaison de moyennes de populations indépendantes avec la fonction t.test

Vidéo éducationnelle: Deux populations indépendantes

Sommaire de la vidéo:
We will assume that you assigned your data to two numerical vectors, say x1 and x2. We will use the t.test to test the equality of means. Its usage is
t.test(x1,x2)
Remarks:
By default, it is testing the null hypothesis that the means are equal against a two-sided alternative that the means are different. To use a one-sided alternative, we can add an argument.
To use a right-sided alternative (i.e. mu1 > m2), add the argument: alternative="greater"
To use a left-sided alternative (i.e. mu1 < m2), add the argument: alternative="less"

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.