MAT1341C, Winter 2017, University of Ottawa - Extra Questions and comments

Geometry behind the dot and cross products

A version in \(\mathbb{R}^2\):

In \(\mathbb{R}^2\), you can really see why the geometric identity for the dot product \[ \vec{u} \cdot \vec{v} = \Vert \vec{u} \Vert \Vert \vec{v} \Vert \cos(\varphi) \] (where \(\varphi\) is the angle between u and v) holds:

Consider a vector \(\vec{v} = (v_1,v_2)\) in \(\mathbb{R}^2\). If its norm is \(\Vert \vec{v}\Vert\) and it makes angle \(\theta\) with the \(x\)-axis, then we can picture it as

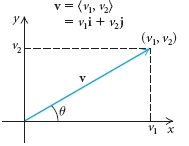
So using trigonometry, we have that \[ v_1 = \Vert \vec{v}\Vert \cos(\theta) \quad \text{and}\quad v_2 = \Vert \vec{v}\Vert\sin(\theta).\]

Similarly, we can write \(\vec{u} = (u_1,u_2) = (\Vert \vec{u}\Vert \cos(\theta'), \Vert \vec{u}\Vert\sin(\theta'))\) where \(\theta'\) is the angle \(\vec{u}\) makes with the positive \(x\)-axis.

So then the angle between \(\vec{u}\) and \(\vec{v}\) is \(\varphi = \vert \theta - \theta'\vert\). Now let's calculate the dot product: \[ \vec{u}\cdot \vec{v} = u_1v_1+u_2v_2 = \Vert \vec{u}\Vert \cos(\theta) \Vert \vec{v}\Vert \cos(\theta') + \Vert \vec{u}\Vert \sin(\theta) \Vert \vec{v}\Vert \sin(\theta') \]

which simplifies, using the difference of angles formula from trigonometry, to \[ = \Vert \vec{u}\Vert \Vert \vec{v}\Vert \left(\cos(\theta) \cos(\theta') - \sin(\theta)\sin(-\theta')\right) = \Vert \vec{u}\Vert \Vert \vec{v}\Vert \cos(\theta - \theta') \] which is what we wanted to show.

Higher dimensions:

In higher dimensions, there are some nice geometric arguments using the cosine law that explain the dot product formula above; for example, here is an Oxford Math Centre site with good pictures.

What about the cross product? Actually the formula \[ \Vert \vec{u}\times \vec{v} \Vert = \Vert \vec{u}\Vert \Vert \vec{v}\Vert \sin(\varphi) \]

is easy to see directly. Remember that \(\vec{u}\times \vec{v} = (yz'-zy', -(xz'-x'z), xy'-y'x)\); so you can write out a formula for \[ \Vert \vec{u}\times \vec{v} \Vert^2 \]

(We square it because it is nicer that way.) The neat trick is to observe that, as expressions in the variables \(x,y,z,x',y',z'\) we have \[ \Vert \vec{u}\times \vec{v} \Vert^2 + (\vec{u}\cdot \vec{v})^2 = \Vert \vec{u}\Vert^2 \Vert \vec{v}\Vert^2\]

which then gives you the identity you want by replacing \( (\vec{u}\cdot \vec{v})^2\) with \( \Vert \vec{u}\Vert^2 \Vert \vec{v}\Vert^2\cos^2(\varphi)\) and using a standard trigonometric identity.

More practice with row reduction

We will keep practicing on Thursday, and will also take the time to examine all the different kinds of cases. For now:

For each of the following problems, set up a system of linear equations, then write down the augmented matrix, and perform row operations (adding a multiple of one row to another, interchanging two rows, or scaling a row by a nonzero constant) to put the system into RREF. Then determine the solution.