Evolution of Carbon in Groundwaters
Fresh groundwaters invariably originate as meteoric waters, in most cases infiltrating through soils and into the geosphere. Along the way, dissolved inorganic carbon (DIC) is gained by dissolution of CO2 and evolves through the weathering of carbonate and silicate parent material. As carbonate acidity is "consumed" by weathering, the pH rises and the distribution of dissolved inorganic carbonate species shifts towards bicarbonate (HCO3) and carbonate (CO32). The groundwater generally approaches equilibrium with calcite, whose solubility will control pH and the equilibrium of carbonate species.
At the same time, labile organic matter from the soil can be dissolved. Oxidation of the dissolved organic matter (DOC) will take initially place by aerobic bacteria that use O2. If the supply of DOC is exhausted before the O2 is consumed, then redox conditions will not evolve much further unless another electron donor in the system is found (ferrous iron minerals, sulphides, etc.). If an excess of DOC accompanies the groundwater below the water table and beyond the influence of atmospheric O2, then anaerobic bacteria will consume it using electron acceptors such as NO3, Fe3+-oxyhydroxides or SO42. Ultimately, methanogenic reactions can take place. Redox evolution is accompanied by mineral dissolution and precipitation reactions that affect the mass balance of dissolved solids and the distribution of isotopes.
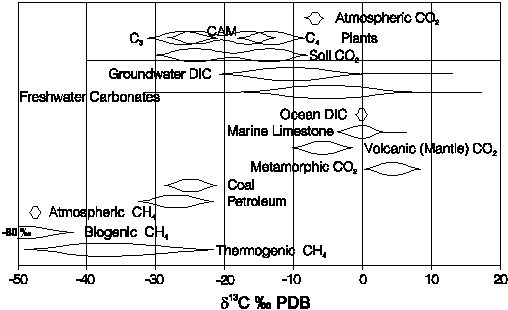
All sources of carbon are linked through these acid-base and redox reactions, which are most often mediated by bacteria. Bacterial involvement is important for two reasons. They derive their energy from redox reactions (usually oxidation of organics), and so act as catalysts, speeding up reactions that are otherwise kinetically impeded. Secondly, bacteria are isotopically selective, preferring to break the weaker, light-isotope bonds. Bacterially mediated reactions are then accompanied by large isotope fractionations. The huge range for d13C in various carbon reservoirs is a demonstration of isotope selectivity by bacteria (Fig. 5-1). Biologically mediated redox reactions for carbon are kinetic, proceeding in one direction only. However, for relatively stable environmental conditions, fractionation is constrained to definable ranges. Understanding the distribution of isotopes in the carbon cycle begins with a look at carbonate geochemistry.

Fig. 5-1 Ranges for d13C values in selected natural compounds. Especially noteworthy is the spread in 13C seen in different plant groups and the resulting soil CO2.
Carbon-13 in the Carbonate System
Carbon-13 is an excellent tracer of carbonate evolution in groundwaters because of the large variations in the various carbon reservoirs. The evolution of DIC and d13CDIC begins with atmospheric CO2 with d13C ~ 7% VPDB. Photosynthetic uptake of CO2(atm) is accompanied by significant depletion in 13C. This occurs during CO2 diffusion into the leaf stomata and dissolution in the cell sap, and during carboxylation (carbon fixation) by the leafs chloroplast, where CO2 is converted to carbohydrate (CH2O). The combination of these fractionating steps results in a 5 to 25 depletion in 13C (Fig). The amount of fractionation depends on the pathway followed. Three principal photosynthetic cycles are recognized: the Calvin or C3 cycle, the Hatch-Slack or C4 cycle, and the Crassulacean acid metabolism (CAM) cycle.
The C3 pathway operates in about 85% of plant species and dominates in most terrestrial ecosystems. C3 plants fix CO2 with the Rubisco enzyme, which also catalyses CO2 respiration through reaction with oxygen. CO2 respiration is an inefficiency that remains as an artifact of evolution in an atmosphere with high CO2 and increasing PO2 (Ehleringer et al., 1991). The diffusion and dissolution of CO2 has a net enrichment in 13C, whereas carboxylation imparts a 29 depletion on the fixed carbon (OLeary, 1988). The result is an overall 13C depletion of about 22. Most C3 plants have d13C values that range from -24 to -30 with an average value of about -27 (Vogel, 1993). The natural vegetation in temperate and high latitude regions is almost exclusively C3. They also dominate in tropical forests. Most major crops are C3, including wheat, rye, barley, legumes, cotton, tobacco, tubers (including sugar beats) and fallow grasses.
The more efficient C4 pathway evolved as atmospheric CO2 concentrations began dropping in the early Tertiary. Under low CO2:O2 conditions and at higher temperatures, increased respiration in C3 plants interferes with their ability to fix CO2. C4 plants add an initial step where the PEP carboxylase enzyme acts to deliver more carbon to Rubisco for fixation. The result is a reduction in 13C fractionation during carboxylation. C4 plants have d13C values that range from -10 to -16, with a mean value of about -12.5 (Vogel, 1993). C4 species represent less than 5% of floral species, but dominate in hot open ecosystems such as tropical and temperate grasslands (Ehleringer et al., 1991). Common agricultural C4 plants include sugar cane, corn and sorghum.
This difference provides a tool to monitor food products marketed as "100% natural", such as fruit juices and maple syrup that can be cut with inexpensive cane sugar. Carbon-13 and other isotopes are now used routinely by customs and excise departments to check the origin of these and other imports (Hillaire-Marcel, 1986).
CAM photosynthesis is favoured by about 10% of plants and dominates in desert ecosystems with plant species such as cacti. They have the ability to switch from C3 photosynthesis during the day to the C4 pathway for fixing CO2 during the night. Their isotopic composition can span the full range of both C3 and C4 plants, but usually is intermediate (Fig. 5-1).
As vegetation dies and accumulates within the soil, decay by aerobic
bacteria converts much of it back to CO2. Soils have CO2
concentrations 10 to 100 times higher than the atmosphere. Microbially-respired
CO2 has much the same d13C
as the vegetation itself. However, outgassing of CO2 along this
steep concentration gradient imparts a diffusive fractionation on the soil
CO2. Cerling et al. (1991) show that measured fractionations
are over 4, and very close to the theoretical fractionation of 4.4 for
CO2 diffusion through air (see page 24). Aravena et al. (1992)
provide addition field evidence for enrichment of soil CO2 by
outward diffusion. For this reason, the d13C
of soil CO2 in most C3 landscapes is generally about
23 (Fig. 5-1). In soils hosting C4 vegetation, it would be
closer to about 9.
The geochemical evolution of groundwaters can involve more than the CO2-based weathering reactions discussed above. Dissolved organic carbon (DOC) plays an important role through reduction-oxidation (redox) reactions. Redox reactions involve the exchange of electrons between two complementary species or redox pairs. One species is oxidized (loss of electrons) and the other is reduced (gain of electrons). Photosynthesis is an example of an endothermic redox reaction, using energy (photons) to reduce carbon from the +IV (oxidized) to the 0 (fixed) redox state:
So what constitutes DOC? The operative boundary between DOC and particulate organic carbon is set as what will pass through a commercially available 0.45-mm filter. The decay products of vegetation form a spectrum of molecular sizes and charges. They are composed of C, O, N, H and S in varying proportions. The most common category of soil-derived organic material are the humic substances, defined as high molecular weight (up to several hundred thousand mass units), refractory, heterogeneous organic substances. In non-contaminated groundwaters, low molecular weight (LMW) compounds make up the rest. LMW DOC includes cellulose, protein, and organic acids such as carboxylic, acetic and amino acids.
The structure and formation of humic substances have yet to be fully understood, and their characterization has been based largely on methods of separation. They are alkali-soluble acids that give the dark colour to soil and wetland waters. Humic acids (HA) precipitate from solution at pH less than 2, while the fulvic acid (FA) fraction is soluble at all pH values. Insoluble humic substances or humin may be that refractory component that is strongly sorbed to the soil mineral component (Stevenson, 1985).
Structurally, humic acids appear to be networks of phenol rings bridged and fringed with carbohydrate, amino acids, fat and protein residues including various O, OH, CH2, NH and S functional groups (Fig. 5-7). Fulvic acids are low molecular weight compounds (Stevenson, 1985; Orlov, 1995).
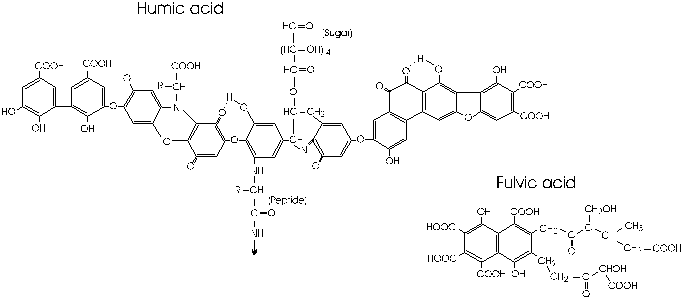
Fig. 5-7 Typical structure of humic and fulvic acids as proposed by Stevenson (1985) and Buffle (1977).
Compositionally, humins are COHNS compounds, varying according to vegetation and decompositional history. Humic acids are roughly 50 to 60% carbon, with 30 to 40% oxygen (Table 5-4). Hydrogen and nitrogen represent on the order of 5% each. Fulvics tend to have slightly lower carbon contents. HA and FA result from the humification of vegetation (cellulose and other carbohydrates, proteins, lignins, tanins etc) by bacterial metabolism and oxidation. Their phenolic and amino acid products then polymerize to form humic substances.
The transport of organic carbon from the soil to groundwater is influenced by soil water conditions and soil structure. DOC in soil moisture reaches a maximum of 10 to 100 mg-C/L in the root zone, and drops off towards the water table (Aiken, 1985). Groundwaters often contain less than 1 to 2 mg-C/L, although groundwaters in certain environments can recharge with much higher DOC concentrations (Wassenaar et al., 1990). Periods of high water table and storm events can flush significant quantities of DOC to the saturated zone, particularly in agricultural areas or in the spring when soil microbial activity is low. Groundwaters recharged through saturated soils, such as in tundra and peat bogs, also typically have high DOC. Groundwaters contaminated with high dissolved organics from landfill sites or septic tanks are another example. In such cases, DOC concentrations can exceed 10 to 100 mg-C/L.
Table 5-4 Mean elemental composition of humic and fulvic acids from
vegetation, soils, surface water and groundwater, in weight percent (from
Thurman, 1985; Orlov, 1995; Steinberg and Muenster, 1985)
| Medium |
|
|
|
|
|
|
|
|
||||||
| Peat |
|
|
|
|
|
|
| Plant residue |
|
|
|
|
|
|
| Humic Acid | ||||||
| Soils |
|
|
|
|
|
|
| Lakes |
|
|
|
|
|
|
| Groundwaters1 |
|
|
|
|
|
|
| Fulvic Acid | ||||||
| Soils |
|
|
|
|
|
|
| Lakes |
|
|
|
|
|
|
| Groundwaters1 |
|
|
|
|
|
|
DOC can also be gained from organic sources within the aquifer. Buried
peat is often a component of Quaternary sediments, and may also be a source
of DOC in groundwaters (Aravena and Wassenaar, 1993). Marine carbonates
and shales can also host sedimentary organic carbon (SOC), ranging from
immature kerogen with elevated O/C ratios to highly reduced, thermally
mature hydrocarbons such as bitumen. Coal horizons, besides having aquifer
potential, can act as a substrate for redox reactions. In most cases, the
d13C value of soil or aquifer-derived
organic carbon is about 25 ± 23 (Fig.
5-1).
The generation of methane by bacteria requires a fully saturated environment that excludes atmospheric O2 and an organic carbon substrate in the absence of other free-energy electron-acceptors such as NO3 and SO42. These conditions are most closely matched by wetlands and Arctic tundra, although bovine digestive tracts also meet the requirements. In natural freshwater systems, the pathways for biological methanogenesis have been reviewed by Klass (1984), and generally involve mixed bacterial populations. Fermentive bacteria begin the process by reducing complex organic structures of carbohydrates, proteins and lipids that originate in vegetation and sediments, to simpler molecules including acetate (CH3COOH), fatty acids, CO2 and H2 gas. In these example reactions from Klass (1984), CH2O is used to represent these complex organic molecules:
6CH2O ® CH3CH2CH2COOH + 2CO2 + 2H2
CH3CH2COOH + 2H2O ® CH3COOH + CO2 + 3H2
The simplified, "pathway-independent" reaction can be written as:
As one might expect, the 13C fractionation between CO2 and CH4 is large (e13CCO2CH4 = 75 ± 15). The metabolic pathway of methanogenic bacteria favours the light isotopes. From Fig. 5-9, biogenic methane in groundwater has d13C values depleted from coexisting CO2 by some 50 to 80. This distinguishes biogenic methane from thermocatalytic and abiogenic origins.
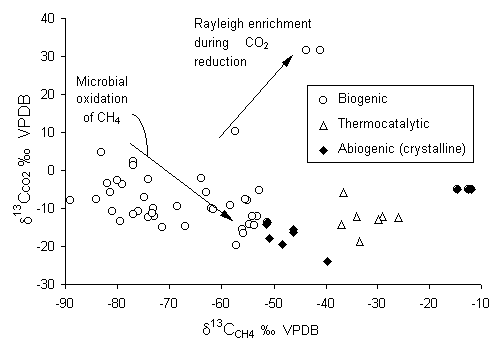
Fig. 5-9 The distribution of 13C between CH4 and coexisting CO2 for fresh and brackish groundwaters with different sources of methane (data from Aravena et al., 1993b; 1995 biogenic; Grossman et al., 1989 biogenic; Barker and Fritz, 1981b biogenic and thermocatalytic; Schoell, 1980 biogenic, Fritz et al., 1987 abiogenic , Fritz et al., 1992 [d13CCH4 > 20] abiogenic).
The fractionation of 2H can also help characterize the source of methane. The 2H contents of methane are established during methanogenesis by the 2H content of the organic substrate and the water participating in the reaction. However, these are kinetic reactions, and the fractionation factors are generally higher than for equilibrium exchange between CH4 and H2O. Deuterium values of -150 to -400 can be measured in the CH4. Subsequent exchange of 2H with water only occurs at geothermal temperatures, well beyond the range of biogenic systems. The combination of d2H and d13C can then be used to distinguish biogenic methane from other sources (Fig. 5-10).
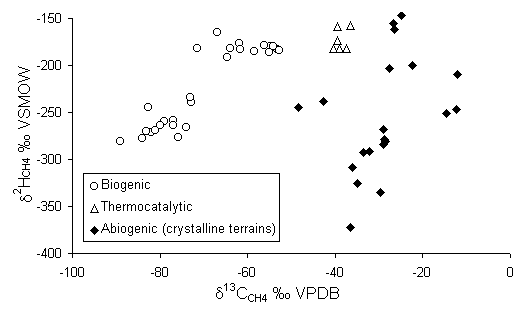
Fig. 5-10 The origin of methane in groundwater according to its d13Cd2H composition (data from Aravena et al., 1995, Grossman et al., 1989, Schoell, 1980 biogenic; Fritz et al., 1987, Sherwood Lollar et al., 1993, Fritz et al., 1992 [d13CCH4 > 20] abiogenic; Barker and Pollock, 1984 thermocatalytic).
The reaction pathway, i.e. acetate fermentation or CO2 reduction, will affect differently the isotopic composition of the methane and the evolution of DIC. A two end-member model was traditionally accepted where CH4 is produced by acetate fermentation in freshwater settings and by CO2 reduction in marine sediments (Whiticar, 1986). In fact methanogenesis by CO2 reduction occurs in many freshwater settings. Using 14C-labeled CO2 and acetate at a freshwater bog, Lansdown et al. (1992) show that their observed CH4 production is essentially via CO2 reduction.
The most diagnostic tool to identify the pathway appears to be the 13C fractionation between coexisting CH4 and CO2, calculated as:
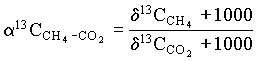
The 13C distribution is also affected by several additional factors. One is the isotopic composition of the organic substrate within the aquifer, which can be preserved in the methane (Grossman et al., 1989). Another is the bacterial oxidation of methane. This produces a positive shift in d13CCH4 and corresponding depletion in the DIC (Fig. 5-11) (Barker and Fritz, 1981a). A positive shift in the 2H content of the CH4 occurs as well.
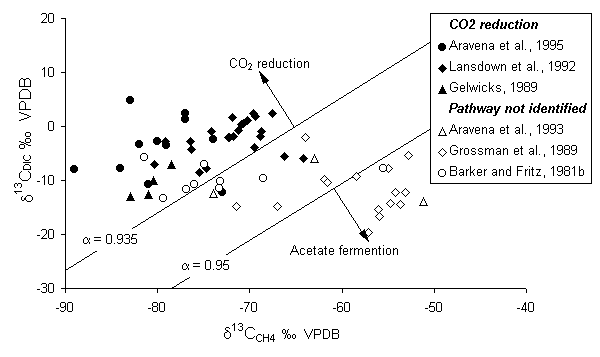
Fig. 5-11 The d13C composition of biogenic methane and CO2 or DIC in groundwater. Filled symbols indicate sites where other evidence indicates CH4 production by CO2 reduction. Fractionation lines for CH4 and CO2 provide an empirical division between the two methanogenic pathways.
Methane oxidation reactions can proceed according to a number of reactions, although the two principal electron acceptors are O2 and SO42. Incorporation of atmospheric O2 generally occurs in the groundwater discharge area such as at the well head, spring vent, or if the groundwaters mix with shallow groundwaters in a phreatic aquifer, oxidizing CH4 according to:
Another important factor is whether the reaction products remain with the groundwater, or are lost (e.g. trapped as a separate gas phase within the aquifer), which may affect Rayleigh type reactions. Brackish groundwaters from 850 m depth in dolomites of the St. Lawrence Lowlands provide an example, where measured d13C values for DIC reach an astounding +31.6 and are ~-41 for CH4 (Fig. 5-9). Such high d13CDIC values are rarely observed in nature, and cannot be attributed to reaction with the dolomites (d13C = +1). In this case, DIC levels are over 600 mg/L (pH = 9.62). DOC reaches 120 mg-C/L and is derived from low-maturity bitumen in the dolomites. TDS reaches 2500 mg/L as NaCl salinity. In this case, reduction of DIC, producing a ~75-depleted CH4 product, imparts a progressive enrichment on the residual DIC pool.
1. What is the pH of a groundwater in equilibrium with a soil atmosphere that has PCO2 = 101.8? The groundwater temperature is 25°C. Determine the distribution of carbonate species (i.e. mH2CO3, mHCO3 and mCO32).
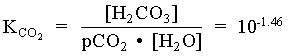
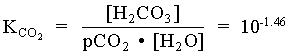
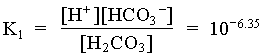
![]()
![]()
mHCO3 = 104.81 = 0.000015 moles/L
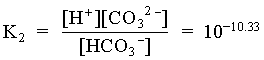
[CO32] = 1010.33 · 104.81 / 104.81 = 1010.33
CO2(g) + H2O « CO2(aq) + H2O « H2CO3 « H+ + HCO3
CO2(g) + H2O « CO2(aq) + H2O « H2CO3
Open system conditions between CaCO3 and CO2(g), and slow growth of calcite to preclude kinetic isotope effects.
Open system conditions between H2O and CaCO3, and slow growth of calcite to preclude kinetic isotope effects.
= 0 + 41.6 = 41.6
Over terrestrial landscape, exchange with 18O-depleted meteoric water would lower the value of d18OCO2. This exchange can take place with condensed moisture, or through exchange with plant water (from soil water) in leaves.
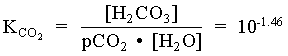
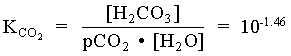
= 101.47 · 101 = 102.47
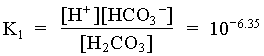
[H+] [HCO3] = [H+]2 = 106.35 · 102.47 = 108.82
In the case where the water had an initial pH of 7.3 and 225 mg/L HCO3, the system can be considered open to the CO2 which must be assumed to be a much larger carbon reservoir than the DIC. As CO2 dissolves and the carbonic acid so formed dissociates, both H+ and HCO3 are added to solution. This supply of H+ will be buffered by the high initial HCO3 concentration. The final HCO3 concentration will then be equal to the initial plus the concentration of H+ added to solution, which maintains a charge balance in the water:
= 102.4 + [H+]
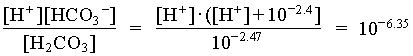
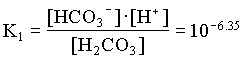
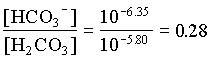
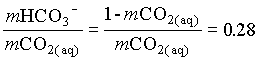
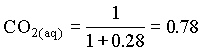
and the fraction of HCO3 = 0.22
Accordingly, the d13C of the DIC for this water is then determined from the isotope mass balance equation using e13C values from Table 5-3:
= 0.22 (23 + 7.9) + 0.78 (-23 1.1)
= 22.1
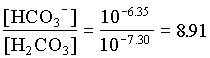
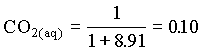
HCO3 = 0.90
d13CDIC = 0.10 (23 1.1) + 0.90 (-23 + 7.9) = 16.0
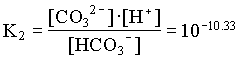
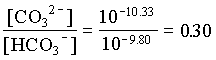
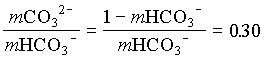
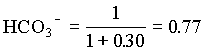
and the fraction of CO32 = 0.23
Accordingly, the d13C of the DIC for this water is then determined from the isotope mass balance equation using e13C values from Table 5-3:
= 0.77 (23 + 7.9) + 0.23 (23 + 7.6)
= 15.2
|
|
5.8 | 7.3 | 9.8 |
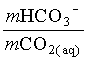 |
|
|
|
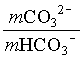 |
|
|
|
| fraction CO2(aq) |
|
|
|
| fraction HCO3 |
|
|
|
| fraction CO32 |
|
|
|
| d13CDIC |
|
|
|
|
|
JR1
|
YK1
|
| pH |
7.31
|
8.35
|
| T |
25
|
5
|
| Ca2+ |
63.0
|
25.5
|
| Mg2+ |
1.3
|
0.3
|
| Na+ |
3.1
|
2.7
|
| HCO3 |
205
|
79.1
|
| SO42 |
<0.5
|
<0.5
|
| Cl |
2.8
|
4.1
|
| d13CDIC |
15.9
|
11.4
|
| JR1 | YK1 | |
| I | 0.005 | 0.0021 |
| gCa | 0.72 | 0.81 |
| gH2CO3 | 1.0 | 1.0 |
| gHCO3 | 0.92 | 0.95 |
| gCO3 | 0.72 | 0.81 |
[Ca2+] = mCa2+ · gCa
= 63.0/40080 · 0.72 = 102.95
[HCO3] = 205/61000 · 0.92 = 102.51
The activities of H2CO3 and CO32 are then determined from the activity of HCO3 and pH:
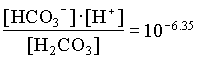
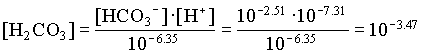
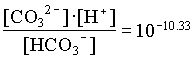
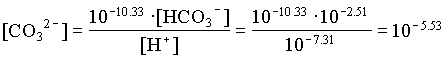
| JR1 | YK1 | |
| [Ca2+] | 102.95 | 103.29 |
| [H2CO3] | 103.47 | 104.74 |
| [HCO3] | 102.51 | 102.91 |
| [CO32] | 105.53 | 105.11 |
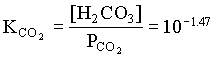
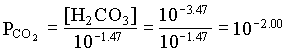
KCaCO3 = 108.48 at 25°C, from Table 5-2
log SICaCO3 = log (IAP/KCaCO3) = log (108.48/108.48) = 0
| JR1 | YK1 | |
| T°C | 25 | 5 |
| PCO2 | 102.00 | 103.55 |
| IAPCaCO3 | 108.48 | 108.39 |
| KCaCO3 | 108.48 | 108.40 |
| log SI | 0.00 | 0.01 |
For JR1, the molalities of the carbonate species are calculated as:
mCO2(aq) = mH2CO3 = [H2CO3] / gH2CO3 = 103.47 / 1 = 0.00039 moles/L
mCO32 = [CO32] / gCO3 = 105.53 / 0.72 = 4.1 · 106 moles/L
+ mHCO3 (d13CCO2(g) + e13CHCO3CO2(g)) + mCO32 (d13CCO2(g) + e13CCO3CO2(g))] / ( mCO2(aq) + mHCO3 + mCO32)
| JR1 | YK1 | |
| T°C |
|
|
| mCO2(aq) |
|
|
| mHCO3 |
|
|
| mCO32 |
|
|
| mDIC |
|
|
| e13CCO2(aq)CO2(g) |
|
|
| e13CHCO3CO2(g) |
|
|
| e13CCO3CO2(g) |
|
|
| d13CDIC (calculated) |
|
|
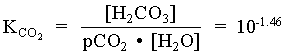
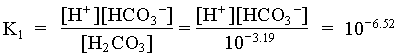
[H+] [HCO3] = [HCO3]2 = 109.71
[HCO3] = 104.86
= 6.46 · 104 + 1.38 · 105 = 6.60 · 104 moles/L
= [6.46 · 104 (23 1.2) + 1.38 · 105 (23 + 10.2)] / (6.46 · 104 + 1.38 · 105)
= 24.0
mDIC mDICrech = 79.1/61000 6.60 · 104 = 6.37 · 104 moles/L
/ ( mDICrech + mCa2+)
= [6.60 · 104 (-24.0) + 6.36 · 104 (1.5)]
/ (6.60 · 104 + 6.36 · 104)
= 11.5
Both the calcites and the DIC will have d13C values that are lower than the original DIC due to additions to the DIC pool from organic carbon. Organic carbon typically has d13C ~ 25 to 30. A mass balance equation can be written to determine the effect on d13CDIC based on the concentration of H2S and DIC in the groundwater.
|
BC1
|
BC2
|
BC3
|
BC4
|
|
| pH |
7.00
|
7.30
|
7.95
|
8.30
|
| T |
10
|
15
|
17
|
18
|
| Ca2+ |
15.3
|
17.0
|
18.9
|
21
|
| Mg2+ |
4.1
|
2.2
|
1.3
|
0.1
|
| Na+ |
7.2
|
12.4
|
14.2
|
18.1
|
| K+ |
2.1
|
2.9
|
3.1
|
3.5
|
| HCO3 |
28.1
|
41.1
|
55.1
|
76.1
|
| SO42 |
32
|
24
|
16
|
0
|
| HS |
0
|
2.8
|
5.5
|
11
|
| Cl |
11
|
12
|
10
|
11
|
| DOC (mg-C/L) |
8
|
6
|
4
|
0
|
| d13CDIC |
15.8
|
17.6
|
18.9
|
21.8
|
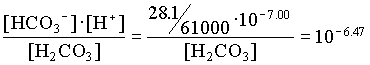
[H2CO3] = 103.34 · 107.00 / 106.47 = 103.87
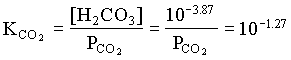
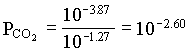
= [10-3.87 · (23 1.1) + 103.34 · (23 + 9.6)] / (10-3.87 + 103.34)
= 15.84
However, the PCO2 in the BC2 to BC4 groundwaters decreases, showing that in this part of the aquifer, weathering takes place under closed system conditions. For the example of BC2:
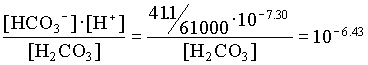
[H2CO3] = 103.17 · 107.30 / 106.43 = 104.04
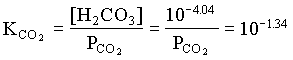
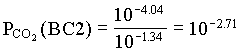
and PCO2 for BC4 = 103.42
As no calcite has been observed in this aquifer, the weathering reactions that have consumed CO2 and increased the pH must be the alteration of primary silicates (see silicate weathering on page 21). The increase in Ca2+ and Na+ would be produced by weathering of feldspars. The sulphate and much of the calcium can be attributed to gypsum dissolution.
Using the appropriate geochemical reactions, show the process responsible for the evolution of DIC and d13CDIC in this groundwater flow system. From your reaction pathway, calculate a final HCO3 concentration and d13CDIC for BC4 and compare with the measured values.
The principal changes we observe in the evolution from BC1 to BC4 are a decrease to 0 in sulphate and DOC, and an increase from 0 to 11 in sulphide. These are the key changes that we would observe during the process of sulphate reduction. The progressive increase in bicarbonate and depletion in 13C is consistent with this.
The geochemical reaction for sulphate reduction can be written as (from Fig. 5-8):
The DIC of BC1 was determined above from HCO3 and pH data:
= (10-3.87 + 103.34) = 103.23 = 5.89 · 104 moles /L
=5.89 · 104 + 2 (2.8/33,000)
= 7.59 · 104 moles/L
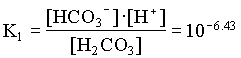
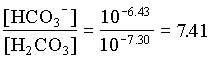
mH2CO3 = mHCO3 / 7.41 = 9.10 · 105 moles/L
Thus, our calculation of mDICBC2, assuming that the increase in bicarbonate is due to sulphate reduction, is the same as that for the actual value determined from measured HCO3 and pH. The same calculations for BC3 and BC4 give the same conclusion that the additions to the DIC pool are derived through sulphate reduction, and oxidation of DOC:
A similar calculation of DIC could be made on the basis of the decrease in DOC for each sample, whereby:
| Sample | pH | mHCO3meas |
|
mDICcalc (H2S) | mDICcalc(DOC) | d13CDIC-meas | d13CDIC-calc |
| BC1 | 7.00 | 4.61 · 104 | 5.89 · 104 |
|
|
|
|
| BC2 | 7.30 | 6.74 · 104 | 7.64 · 104 | 7.65 · 104 | 7.56 · 104 |
|
|
| BC3 | 7.95 | 9.03 · 104 | 9.29 · 104 | 9.22 · 104 | 9.22 · 104 |
|
|
| BC4 | 8.30 | 12.48 · 104 | 12.64 · 104 | 12.56 · 104 | 12.56 · 104 |
|
|
|
FR1
|
FR2
|
FR3
|
FR4
|
|
| pH |
8.05
|
7.85
|
7.50
|
7.42
|
| T |
5.1
|
5.1
|
5.1
|
5.1
|
| Eh (mV) |
325
|
175
|
213
|
207
|
| Ca2+ |
31
|
48
|
61
|
68
|
| Mg2+ |
1.9
|
1.8
|
2.1
|
1.7
|
| Na+ |
2.4
|
3.2
|
1.8
|
2.9
|
| HCO3 |
108
|
163
|
199
|
223
|
| SO42 |
<0.5
|
<0.5
|
<0.5
|
<0.5
|
| Cl |
3
|
2
|
4
|
3
|
| DOC (mg-C/L) |
44
|
28
|
12
|
2
|
| CH4 |
0
|
21
|
43
|
56
|
| d 13CDIC |
13.7
|
2.1
|
3.1
|
5.2
|
In fresh waters, it is the CO2- reduction reaction pathway that dominates:
Giving the overall reaction:
Ionic strength: ![]()
Activity coefficients: ![]()
Ion activities: [Ca2+] = mCa2+ · gCa
[HCO3] = (mgHCO3/L)/61,000 · gHCO3
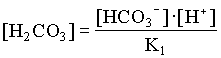
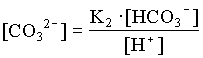
mDIC = mHCO3 + mCO2(aq)
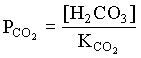
pKCO2 = 1.19
pK2 = 10.55
pKCaCO3 = 8.39
| FR1 | FR2 | FR3 | FR4 | |
| I | 0.0027 | 0.0040 | 0.0050 | 0.0055 |
| gCa | 0.78 | 0.74 | 0.72 | 0.71 |
| gHCO3 | 0.94 | 0.93 | 0.92 | 0.92 |
| gCO3 | 0.78 | 0.74 | 0.72 | 0.71 |
| [Ca2+] | 103.22 | 103.07 | 102.96 | 102.92 |
| [H2CO3] | 104.27 | 103.61 | 103.13 | 103.00 |
| [HCO3] | 102.78 | 102.60 | 102.52 | 102.48 |
| [CO32] | 105.37 | 105.88 | 106.07 | 106.07 |
| mCO2(aq) | 5.21 · 105 | 2.33 · 104 | 6.36 · 104 | 8.37 · 104 |
| mHCO3 | 1.76 · 103 | 2.68 · 103 | 3.26 · 103 | 3.65 · 103 |
| mDIC | 1.81 · 103 | 2.91 · 103 | 3.90 · 103 | 4.49 · 103 |
| mCa2+ | 5.08 · 104 | 7.87 · 104 | 1.00 · 103 | 1.11 · 103 |
| log PCO2 | 3.11 | 2.44 | 1.96 | 1.84 |
| log SICaCO3 | 0.05 | 0.35 | 0.42 | 0.36 |
The d13C of the DIC in FR1 can be calculated using the closed system approach we saw in problem 7 for YK1. First, we calculate mDICrech from the soil PCO2 of 101.8 and then the d13C of DIC in the recharge water prior to closed system dissolution of calcite. Enrichment values are from Table 5-3, for 5°C:
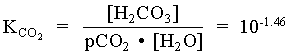
[H2CO3] = [CO2(aq)] = mCO2(aq) = 102.99 = 1.02 · 103 moles/L
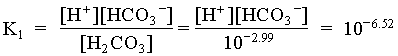
[H+] [HCO3] = [HCO3]2 = 109.51
[HCO3] = 104.76
= 1.02 · 103 + 1.74 · 105 = 1.04 · 103 moles/L
= (23 1.2)
= 24.2
/ ( mDICrech + mCa2+)
= [1.04 · 103 (-24.2) + 7.73 · 104 (0)] / (1.04 · 103 + 7.73 · 104)
= 13.9
The enrichment in d13C observed in FR2, FR3 and FR4 was attributed to the strong fractionation due to methanogenesis. During bacterial CO2 reduction (see equation above) 12CO2 is preferentially used over 13CO2. The enrichment factor e13CCO2CH4 is between 60 and 90 (Whiticar et al., 1986). The 13C enrichment in the residual DIC during this reaction can be likened to a Rayleigh distillation. It is for this reason that d13C enrichments DIC in methanogenic groundwaters can reach 20 and more (Fig. 5-9). This can be simulated on the basis of a d13C mass balance equation and Rayleigh equation.
The approach is to calculate the total DIC reservoir which will be equal to the DIC from previous sample (mDICFR1), plus the amount of DOC oxidized (DDOC) plus the amount of carbonate dissolved (DCa2+). The ratio of this calculation of total DIC to actual DIC (after CO2 reduction and generation of CH4) represents the residual fraction, f, for the Rayleigh calculation. The 13C fractionation factor during methanogenesis can be set at a median value of say e13CCO2CH4 = 75. The value of d13CDOC is set at 26 and the aquifer carbonate has d13Ccarb = 0.
Here we will run through this calculation for FR2, which is the first of the series to show evidence of methanogenesis. The d13C of the total DIC pool prior to CO2 reduction is then determined from the Rayleigh equation:
d13CDICFR2 = d13CDICinit e13CCO2CH4 · ln (mDICFR2 / mDICinit)
For this calculation:
mDICFR2 = 2.91 · 103 moles/L (from table above)
= 1.81 · 103 + 1.33 · 103 + 4.24 · 104
= 3.57 · 103 moles/L
f = mDICFR2 / mDICinit
= 2.91 · 103 / 3.57 · 103
= 0.815
= [13.7 · 1.81 · 103 + (26) · 1.33 · 103 + (0) · 4.24 · 104] / [1.81 · 103 + 1.33 · 103 + 4.24 · 104]
= 16.7
= 16.7 75 · ln (2.91 · 103 / 3.57 · 103)
= 16.7 75 · ln (0.815)
= 1.36
This value is close to the measured value for FR2 of 2.1, and so our interpretation of a rayleigh enrichment during CO2 reduction must be correct.
Carrying out these calculations for FR3 and FR4 also produce values similar to those measured:
= 4.57 · 103 moles/L
= [2.1 · 2.91 · 103 + (26) · 1.33 · 103] / [2.91 · 103 + 1.33 · 103 + 3.24 · 104]
= 8.91 75 · ln (3.90 · 103 / 4.57 · 103)
= 3.0
= 4.90 · 103 moles/L
= [3.1 · 3.90 · 103 + (26) · 8.33 · 104] / [3.90 · 103 + 8.33 · 104 + 1.74 · 104]
= 1.95 75 · ln (4.49 · 103 / 4.90 · 103)
= 4.6